Question

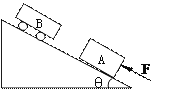
【题目】不计质量的弹簧，圆弧AB部分光滑，半径为R，平面BC部分粗糙，长为l，C点右方的平面光滑．滑块质量为m，从圆弧最高处A无初速下滑（如图），与弹簧相接触并压缩弹簧，最后又返回到B相对于车静止．求：

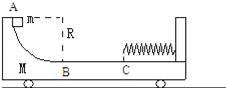
（1）BC部分的动摩擦因数μ；

（2）弹簧具有的最大弹性势能；

（3）当滑块与弹簧刚分离时滑块和小车的速度大小．

Answer 1

【答案】（1） ；（2）；（3） ，

【解析】（1）滑块与小车初始状态为静止，末状态滑块相对小车静止，据能量守恒定律可得：mgR=μmg2l
解得
（2）弹簧压缩到最大形变量时，滑块与小车共速，根据动量守恒定律可知共同速度为0，据能量守恒，弹簧的弹性势能为：EP＝mgRμmgl＝mgR

（3）弹簧与滑块分离的时候，弹簧的弹性能为0，设此时滑块速度为v1，小车速度为v2据能量守恒有：

系统动量守恒，有：mv1-Mv2=0
解得：，