题目内容
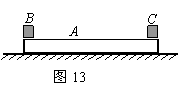
 如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)
如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)(1)在此过程中A的最大速度是多大?
(2)此过程中内能增加了多少?
(3)为使B、C不相撞,木板的长度至少为多长?
分析:(1)通过A、B对长木板摩擦力的大小比较,确定长木板A是否和B一起做加速运动,分别求得A与C的加速度,计算出A的最大速度;
(2)最终三者的共同速度由动量守恒求得共同的速度,内能的增加量等于系统减少的动能;
(3)结合牛顿第二定律和运动学公式求出C与长木板相对静止时,它们的相对位移的大小;全过程中A与B的相对位移,为使B、C不相撞,木板的最小长度为B、C相对A的位移的和.
(2)最终三者的共同速度由动量守恒求得共同的速度,内能的增加量等于系统减少的动能;
(3)结合牛顿第二定律和运动学公式求出C与长木板相对静止时,它们的相对位移的大小;全过程中A与B的相对位移,为使B、C不相撞,木板的最小长度为B、C相对A的位移的和.
解答:解:(1)C的加速度为ac=μg=5 m/s2;
若A、B之间不滑动,则A、B一起加速运动,加速度为aAB=
=
=
>μg=5
故假设不成立,即A、B之间存在相对滑动.这样A的加速度aA=
=
m/s2=15m/s2,方向向右;
B的加速度为aB=μg=5m/s2,方向向右;
设A、C经过时间t后速度均变为v,则v=8-5t=15t,所以t=0.4 s;此时的速度即为A的最大速度,故v=6 m/s;
(2)最终三者的共同速度由动量守恒mcv0=(mA+mB+mC)v
可得:v=5 m/s,
故内能的增加量为△E=
mCv02-
(mA+mB+mC)v2=60J;
(3)首先是C与A的相对滑动,A、C之间相对滑动的距离sCA=sC-sA=v0t-
aCt2-
aAt2=1.6 m;
此时A、C不再相对滑动,
当A与C相对静止后,B与A仍有相对滑动,B与A的总的相对滑动距离可由能量守恒求得:
Q=μmBgsAB+μmCgsAC=60得:sAB=2 m;
所以木板的最小长度为L=sAB+sAC=3.6 m
答:(1)在此过程中A的最大速度是6m/s;
(2)此过程中内能增加了60J;
(3)为使B、C不相撞,木板的长度至少为3.6m.
若A、B之间不滑动,则A、B一起加速运动,加速度为aAB=
| μmCg |
| mA+mB |
| 0.5×5×10 |
| 1+2 |
| 25 |
| 3 |
故假设不成立,即A、B之间存在相对滑动.这样A的加速度aA=
| μg(mC-mB) |
| mA |
| 0.5×10×(5-2) |
| 1 |
B的加速度为aB=μg=5m/s2,方向向右;
设A、C经过时间t后速度均变为v,则v=8-5t=15t,所以t=0.4 s;此时的速度即为A的最大速度,故v=6 m/s;
(2)最终三者的共同速度由动量守恒mcv0=(mA+mB+mC)v
可得:v=5 m/s,
故内能的增加量为△E=
| 1 |
| 2 |
| 1 |
| 2 |
(3)首先是C与A的相对滑动,A、C之间相对滑动的距离sCA=sC-sA=v0t-
| 1 |
| 2 |
| 1 |
| 2 |
此时A、C不再相对滑动,
当A与C相对静止后,B与A仍有相对滑动,B与A的总的相对滑动距离可由能量守恒求得:
Q=μmBgsAB+μmCgsAC=60得:sAB=2 m;
所以木板的最小长度为L=sAB+sAC=3.6 m
答:(1)在此过程中A的最大速度是6m/s;
(2)此过程中内能增加了60J;
(3)为使B、C不相撞,木板的长度至少为3.6m.
点评:解决本题的关键能够正确地受力分析,结合牛顿第二定律和运动学公式,以及动量守恒定律进行求解.该题的过程多,难度大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,水平面C点以左是光滑的,C点以右是粗糙的,A、B两物体之间用轻质弹簧连接,用水平恒力F拉A,使A、B一起沿光滑水平面做匀加速运动,这时弹簧长度为L1;接着它们先后过C点进入表面粗糙的水平面后,A、B还是一起做匀加速运动,此时弹簧长度为L2.若A、B与粗糙水平面之间的动摩擦因数相同,则下列关系式正确的是( )
如图所示,水平面C点以左是光滑的,C点以右是粗糙的,A、B两物体之间用轻质弹簧连接,用水平恒力F拉A,使A、B一起沿光滑水平面做匀加速运动,这时弹簧长度为L1;接着它们先后过C点进入表面粗糙的水平面后,A、B还是一起做匀加速运动,此时弹簧长度为L2.若A、B与粗糙水平面之间的动摩擦因数相同,则下列关系式正确的是( ) 如图所示,水平面内有两根互相平行且足够长的光滑金属轨道,它们间的距离L=0.20m,在两轨道的左端之间接有一个R=0.10Ω的电阻.在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T.一根质量m=0.10kg的直金属杆ab垂直于轨道放在两根轨道上.某时刻杆ab以v0=2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以a=2.0m/s2的加速度做匀减速直线运动.杆ab始终与轨道垂直且它们之间保持良好接触.杆ab和轨道的电阻均可忽略.
如图所示,水平面内有两根互相平行且足够长的光滑金属轨道,它们间的距离L=0.20m,在两轨道的左端之间接有一个R=0.10Ω的电阻.在虚线OO′(OO′垂直于轨道)右侧有方向竖直向下的匀强磁场,磁感应强度B=0.50T.一根质量m=0.10kg的直金属杆ab垂直于轨道放在两根轨道上.某时刻杆ab以v0=2.0m/s且平行于轨道的初速度进入磁场,同时在杆上施加一个水平拉力,使其以a=2.0m/s2的加速度做匀减速直线运动.杆ab始终与轨道垂直且它们之间保持良好接触.杆ab和轨道的电阻均可忽略.