题目内容
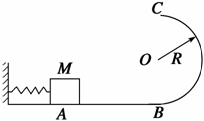
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物块(可视为质点)将弹簧压缩至A点后由静止释放,在弹力作用下物块获得某一向右速度后脱离弹簧,当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动恰能完成半个圆周运动到达C点.试求:

(1)弹簧开始时的弹性势能;
(2)物块从B点运动至C点克服阻力做的功;
(3)物块离开C点后落回水平面时的动能.
【答案】
3mgR ;0.5mgR ;2.5mgR
【解析】
试题分析:(1)物块在B点时,
由牛顿第二定律得:FN-mg=m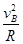 ,FN=7mg
,FN=7mg
EkB=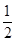 mvB2=3mgR
mvB2=3mgR
在物体从A点至B点的过程中,根据机械能守恒定律,弹簧的弹性势能Ep=EkB=3mgR.
(2)物体到达C点仅受重力mg, 根据牛顿第二定律有:
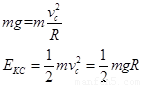
物体从B点到C点只有重力和阻力做功,根据动能定理有:
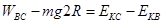
解得: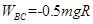
所以物体从B点运动至C点克服阻力做的功为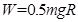
(3)物体离开轨道后做平抛运动,水平方向有: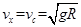 ,竖直方向速度为
,竖直方向速度为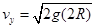 ,所以根据
,所以根据 则
则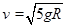 ,所以
,所以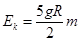
考点:机械能守恒定律、动能定理、圆周运动过最高点条件、平抛运动
点评:此类题型考察了多过程问题,先通过机械能守恒定律判断被弹出物体的动能,然后利用动能定理解决变速曲线运动,最后利用平抛运动规律解决问题。在使用机械能守恒定律之前应首先判断是否满足机械能守恒条件:看看是否产生机械能之外的其他能量,若有则机械能不守恒,反之则守恒。

练习册系列答案
相关题目
 如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)
如图所示光滑水平面有一长木板其质量为mA=1kg,长木板两端有两小物块.其质量分别为mB=2kg,mc=5kg,已知B与A之间、C与A之间的动摩擦因数均为μ=O.5,现物块C以初速度V.=8m/s向左运动,最终物体C恰好没有与B相碰(g=10m/s2,B、C均可看成质点)