题目内容
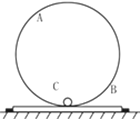
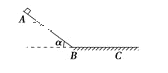
【题目】如图所示,一个固定在竖直平面内的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3 s后又恰好垂直与倾角为45°的斜面相碰。已知半圆形管道的半径为R=1 m,小球可看做质点且其质量为m=1 kg,g取10 m/s2。则( )

A. 小球在斜面上的相碰点C与B点的水平距离是1.9 m
B. 小球在斜面上的相碰点C与B点的水平距离是0.9 m
C. 小球经过管道的B点时,受到管道的作用力FNB的大小是1 N
D. 小球经过管道的A点时,受到管道的作用力FNA的大小是59N
【答案】BCD
【解析】
根据平抛运动的规律和运动合成的可知:tan45°=![]() ,则小球在C点竖直方向的分速度和水平分速度相等,得:vx=vy=gt=3m/s,则B点与C点的水平距离为:x=vxt=3×0.3=0.9m;故B正确,A错误;B点的速度为3m/s,根据牛顿运动定律,在B点设轨道对球的作用力方向向下;FNB+mg=
,则小球在C点竖直方向的分速度和水平分速度相等,得:vx=vy=gt=3m/s,则B点与C点的水平距离为:x=vxt=3×0.3=0.9m;故B正确,A错误;B点的速度为3m/s,根据牛顿运动定律,在B点设轨道对球的作用力方向向下;FNB+mg=![]() ,代入解得:NB=-1N负号表示轨道对球的作用力方向向上,故C正确。小球在A点的速度:
,代入解得:NB=-1N负号表示轨道对球的作用力方向向上,故C正确。小球在A点的速度:![]() ,解得vA=7m/s,则A点由牛顿第二定律:
,解得vA=7m/s,则A点由牛顿第二定律:![]() 解得NA=59N,选项D正确; 故选BCD。
解得NA=59N,选项D正确; 故选BCD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目