题目内容
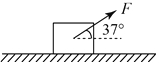
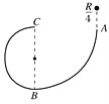
【题目】如图所示，在倾角为θ=30°的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为m和2m，弹簧的劲度系数为k，C为一固定挡板，开始时系统处于静止状态，现用一沿斜面向上的力F拉物块A使之向上做匀加速运动，直到物块B刚要离开C（g取10m/s2）。求：
（1）物块B刚要离开C时弹簧弹力F
；
（2）当物块B刚要离开C时F=2mg，求上述过程中物块A运动时间？
【答案】（1）mg；（2）
【解析】（1）用x1表示未加F时弹簧的压缩量，由胡克定律和牛顿第二定律可知，
mgsin30°=kx1
用x2表示B刚要离开C时弹簧的伸长量，a表示此时A的加速度，由胡克定律和牛顿第二定律F0=kx2=2mgsin30°，则F0=mg
（2）对A:F-mgsin30°-kx2=ma
将F=2mg代入得：a=0.5g
由x1+x2=
at2
t=
优质课堂快乐成长系列答案【题目】用如图甲所示的实验装置来验证牛顿第二定律。
（1）为消除摩擦力的影响，实验前必须进行平衡摩擦力。莱同学平衡摩擦力时是这样操作的：将小车水平静止地放在长木板上，把木板不带滑轮的一端垫高(如图乙)，让小车由静止开始沿木板向下滑动。请问这位同学的操作是否正确? 如果不正确，应当如何操作? 答：________________________________。
(2)如果这位同学按(1)的步骤操作，然后不断改变对小车的拉力F，他得到的小车质量M不变情况下的a-F图线是下列图中的_____________。
A.
B.
C.
D.
（3)另一位同学按照正确的实验步骤操作，计算出各纸带的加速度，将测得的加速度a和F的有关数据记录在下表中。请根据表中所列数据画出-F图线，由图线可知M=___________kg.(结果保留两位有效数字)
a/（ms-2） | 1.98 | 4.00 | 5.97 | 8.02 |
F/N | 1.00 | 2.00 | 3.00 | 4.00 |
