Question

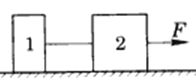
【题目】如图所示，1、2两木块用绷直的细绳连接，放在水平面上，其质量分别为ｍ1＝1.0ｋｇ、ｍ2＝2.0ｋｇ，它们与水平面间的动摩擦因数均为μ＝0.10．在ｔ＝0时开始用向右的水平拉力Ｆ＝6.0Ｎ拉木块2和木块1同时开始运动，过一段时间细绳断开，到ｔ＝6.0ｓ时1、2两木块相距Δｓ＝22.0ｍ（细绳长度可忽略），木块1早已停止．求此时木块2的动能．（ｇ取10ｍ／ｓ2）

Answer 1

【答案】100Ｊ

【解析】对系统

对木块1，细绳断后：│ａ1│＝μｇ＝1ｍ／ｓ2

设细绳断裂时刻为ｔ1，则木块1运动的总位移：ｓ1＝2ａ0ｔ12＝ａ0ｔ12．

对木块2，细绳断后，ａ2＝＝2ｍ／ｓ2．

木块2总位移

ｓ2＝ｓ′＋ｓ″＝ａ0ｔ12＋ｖ1（6－ｔ1）＋ａ2（6－ｔ1）2

两木块位移差Δｓ＝ｓ2－ｓ1＝22（ｍ）．

得ａ0ｔ12＋ｖ1（6－ｔ1）＋ａ2（6－ｔ1）2－ａ0ｔ12＝22，

把ａ0，ａ2值，ｖ1＝ａ0ｔ1代入上式整理得：ｔ12＋12ｔ1－28＝0，得ｔ1＝2ｓ．

木块2末速ｖ2＝ｖ1＋ａ2（6－ｔ1）＝ａ0ｔ1＋ａ2（6－ｔ1）＝10ｍ／ｓ．

此时动能Ｅｋ＝ｍ2ｖ22＝×2×102Ｊ＝100Ｊ．