题目内容
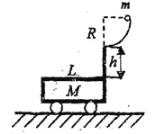
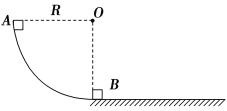
【题目】如图所示,竖直平面内的四分之一圆弧轨道下端与水平桌面相切,小滑块A和B分别静止在圆弧轨道的最高点和最低点.现将A无初速释放,A与B碰撞后结合为一个整体,并沿桌面滑动.已知圆弧轨道光滑,半径R;A和B的质量均为m;A和B整体与桌面之间的动摩擦因数μ.重力加速度为g.求:
(1)碰撞前A对轨道的压力大小;
(2)A和B整体在桌面上滑动的距离l.
【答案】(1)3mg(2)![]()
【解析】
(1)可根据动能定理或机械能守恒来求解A与B碰撞前一瞬间时的速度大小,利用牛顿第二定律和第三定律来求解A对轨道的压力大小;(2)A、B碰撞的过程动量守恒,碰后以共同速度开始在地面上减速,可对AB整体运用动能定理求解滑行距离![]() 。
。
(1)根据机械能守恒定律有![]()
由圆周运动规律有![]()
FN =3mg ; 由牛顿第三定律有F压= FN =3mg
(2)根据动量守恒定律有mv=2mv′
根据动能定理有![]()
解得A和B整体沿水平桌面滑动的距离![]() 。
。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目