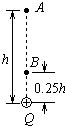题目内容
如图所示,带电荷量为Q的正点电荷固定在倾角为30°的光滑绝缘斜面底部的C点,斜面上有A、B两点,且A、B和C在同一直线上,A和C相距为L,B为AC中点.现将一带电小球从A点由静止释放,当带电小球运动到B点时速度正好又为零,已知带电小球在A点处的加速度大小为
,静电力常量为k,求:
(1)小球运动到B点时的加速度大小.
(2)B和A两点间的电势差(用Q和L表示).

| g |
| 4 |
(1)小球运动到B点时的加速度大小.
(2)B和A两点间的电势差(用Q和L表示).

(1)根据牛顿第二定律和库仑定律得:
带电小球在A点时有:
mgsin 30°-k
| L2 |
带电小球在B点时有:
k
(
|
且aA=
| g |
| 4 |
| g |
| 2 |
(2)由A点到B点应用动能定理得:
mgsin 30°?
| L |
| 2 |
由mgsin 30°-k
| L2 |
| g |
| 4 |
可得:
| 1 |
| 4 |
| L2 |
可求得:UBA=k
| Q |
| L |
答:
(1)小球运动到B点时的加速度大小为
| g |
| 2 |
(2)B和A两点间的电势差为k
| Q |
| L |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目