ΧβΡΩΡΎ»ί
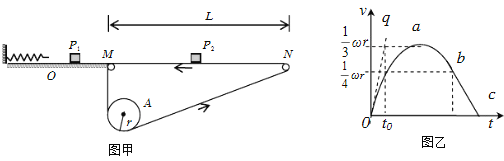
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§MN «ΑκΨΕΈΣRΒΡ![]() ΙβΜ§‘≤ΜΓΘ§ΡΨΑεBΨ≤÷Ι‘ΎΥ°ΤΫΟφ…œΘ§ΤδΉσΕΥ”κNΒψ÷ΊΚœΘ§”“ΕΥΖ≈”–Μ§ΩιAΓΘΜ§ΩιC¥”PΒψ”…Ψ≤÷Ι ΆΖ≈Θ§«Γ¥”MΒψ«–»κ‘≤ΙλΒάΘ§”κΡΨΑεB≈ωΉ≤Κσ’≥ΈΣ“ΜΧεΘ§≈ωΉ≤ ±ΦδΦΪΕΧΘ§÷°ΚσΘ§BΓΔC“ΜΤπ―ΊΥ°ΤΫΟφ‘ΥΕ·Θ§Μ§ΩιA«ΓΚΟΈ¥¥”B…œΒτœ¬ΓΘ“―÷ΣΜ§ΩιAΓΔCΒΡ÷ ΝΩΨυΈΣmΘ§ΡΨΑεBΒΡ÷ ΝΩΈΣ2mΘ§Μ§ΩιA”κΡΨΑεB÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΈΣΠΧ1Θ§Μ§ΩιCΚΆΡΨΑεB”κΒΊΟφ÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΨυΈΣ
ΙβΜ§‘≤ΜΓΘ§ΡΨΑεBΨ≤÷Ι‘ΎΥ°ΤΫΟφ…œΘ§ΤδΉσΕΥ”κNΒψ÷ΊΚœΘ§”“ΕΥΖ≈”–Μ§ΩιAΓΘΜ§ΩιC¥”PΒψ”…Ψ≤÷Ι ΆΖ≈Θ§«Γ¥”MΒψ«–»κ‘≤ΙλΒάΘ§”κΡΨΑεB≈ωΉ≤Κσ’≥ΈΣ“ΜΧεΘ§≈ωΉ≤ ±ΦδΦΪΕΧΘ§÷°ΚσΘ§BΓΔC“ΜΤπ―ΊΥ°ΤΫΟφ‘ΥΕ·Θ§Μ§ΩιA«ΓΚΟΈ¥¥”B…œΒτœ¬ΓΘ“―÷ΣΜ§ΩιAΓΔCΒΡ÷ ΝΩΨυΈΣmΘ§ΡΨΑεBΒΡ÷ ΝΩΈΣ2mΘ§Μ§ΩιA”κΡΨΑεB÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΈΣΠΧ1Θ§Μ§ΩιCΚΆΡΨΑεB”κΒΊΟφ÷°ΦδΒΡΕ·ΡΠ≤Ν“ρ ΐΨυΈΣ![]() Θ§Μ§ΩιAΓΔΜ§ΩιCΨυΩ… ”ΈΣ÷ ΒψΘ§÷ΊΝΠΦ”ΥΌΕ»ΈΣgΘ§Κω¬‘Ω’ΤχΉηΝΠΘ§Υ°ΤΫΟφΉψΙΜ≥ΛΓΘ
Θ§Μ§ΩιAΓΔΜ§ΩιCΨυΩ… ”ΈΣ÷ ΒψΘ§÷ΊΝΠΦ”ΥΌΕ»ΈΣgΘ§Κω¬‘Ω’ΤχΉηΝΠΘ§Υ°ΤΫΟφΉψΙΜ≥ΛΓΘ
«σΘΚ(1)Μ§ΩιCΨ≠NΒψ ±”κΡΨΑεB≈ωΉ≤«ΑΒΡΥ≤ΦδΕ‘‘≤ΜΓΙλΒάΒΡ―ΙΝΠΓΘ
(2)Μ§ΩιAΆΘ÷Ι ±ΒΫNΒψΒΡΥ°ΤΫΨύάκΓΘ
ΓΨ¥πΑΗΓΩ(1) ![]() Θ§ΖΫœρ ζ÷±œρœ¬ΓΘ (2)»τ
Θ§ΖΫœρ ζ÷±œρœ¬ΓΘ (2)»τ![]() ,‘ρΥ°ΤΫΨύάκΈΣ:
,‘ρΥ°ΤΫΨύάκΈΣ: ![]() Μρ
Μρ![]() ΘΜ»τ
ΘΜ»τ![]() ,‘ρΥ°ΤΫΨύάκΈΣ:
,‘ρΥ°ΤΫΨύάκΈΣ: ![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
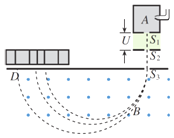
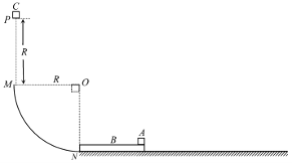
Θ®1Θ©”…Ε·ΡήΕ®άμ«σ≥ω–Γ«ρΒΫNΒψΒΡΥΌΕ»Θ§”…≈ΘΕΌΒΎΕΰΕ®¬…«σ≥ω‘ΎNΒψ ήΒΫΒΡ÷ß≥÷ΝΠΘ§”…≈ΘΕΌΒΎ»ΐΕ®¬…ΒΟ≥ω≈ωΉ≤«ΑΒΡΥ≤ΦδΕ‘‘≤ΜΓΙλΒάΒΡ―ΙΝΠΘΜ
Θ®2Θ©Μ§ΩιC≈ωΡΨΑεBΒΡΙΐ≥Χ÷–Θ§”…Ε·ΝΩ ΊΚψΕ®¬…Ω…«σ≈ωΚσΒΡΥΌΕ»ΓΘΜ§ΩιA«ΓΚΟ‘ΥΕ·ΒΫΡΨΑεBΒΡΉσΕΥ ±Θ§ABC¥οΒΫΙ≤Ά§ΥΌΕ»vΘ§ΗυΨί‘ΥΕ·―ßΙΪ ΫΖ÷±π«σ≥ω¥ΥΙΐ≥ΧΒΡ ±ΦδΚΆΥΌΕ»ΓΘ“‘Κσ‘ΥΕ·ΗυΨίœύΜΞΦδΒΡΡΠ≤ΝΝΠ¥σ–Γ≤ΜΆ§Θ§Ζ÷ΝΫ÷÷«ιΩω«σ≥ωΜ§ΩιΜ§Ε·ΒΡΨύάκΘ§ΉνΚσ«σ≥ωΜ§ΩιAΆΘ÷Ι ±ΨύNΒψΒΡΥ°ΤΫΦδΨύΓΘ
Θ®1Θ©Μ§ΩιC”…PΒΫNΒΡΙΐ≥Χ÷–Θ§”…Ε·ΡήΕ®άμΒΟ
![]()
‘ΎNΒψΘ§”…≈ΘΕΌΒΎΕΰΕ®¬…ΒΟΘΚ![]()
ΫβΒΟFN=5mg
”…≈ΘΕΌΒΎ»ΐΕ®¬…ΒΟΘ§Μ§ΩιCΨ≠NΒψ ±”κΡΨΑεB≈ωΉ≤«ΑΒΡΥ≤ΦδΕ‘‘≤ΜΓΙλΒάΒΡ―ΙΝΠ¥σ–ΓΈΣ5mgΘ§ΖΫœρ ζ÷±œρœ¬ΓΘ
Θ®2Θ©Μ§ΩιC≈ωΡΨΑεBΒΡΙΐ≥Χ÷–Θ§Ε·ΝΩ ΊΚψΓΘ…η≈ωΚσΥ≤ΦδΘ§BΓΔCΒΡΙ≤Ά§ΥΌΕ»ΈΣv0Θ§‘ρΘΚ
mvN=Θ®m+2mΘ©v0
Ε‘Μ§ΩιA”–ΘΚ![]()
Ε‘BC”–ΘΚ![]()
Μ§ΩιA«ΓΚΟ≤ΜΒτœ¬Θ§Μ§ΩιA«ΓΚΟ‘ΥΕ·ΒΫΡΨΑεBΒΡΉσΕΥ ±Θ§ABC¥οΒΫΙ≤Ά§ΥΌΕ»vΘ§…η¥ΥΙΐ≥Χ”Ο ±tΘ§‘ρ”–ΘΚ
![]()
![]()
Μ§ΩιAΒΡΈΜ“ΤΈΣΘΚ![]()
Μ§ΩιBCΒΡΈΜ“ΤΈΣΘΚ![]()
…ηΡΨΑε≥ΛΕ»ΈΣlΘ§”…ΦΗΚΈΙΊœΒΒΟΘΚ![]()
ΝΣΝΔΫβΒΟΘΚ![]()
![]()
![]()
ΔΌ»τ![]() Θ§‘ρAΓΔBΓΔC¥οΒΫΙ≤Ά§ΥΌΕ»vΚσ“ΜΤπ‘»ΦθΥΌΒΫΥΌΕ»ΈΣ0Θ§”–ΘΚ
Θ§‘ρAΓΔBΓΔC¥οΒΫΙ≤Ά§ΥΌΕ»vΚσ“ΜΤπ‘»ΦθΥΌΒΫΥΌΕ»ΈΣ0Θ§”–ΘΚ
![]()
Μ§ΩιAΆΘ÷Ι ±ΨύNΒψΒΡΥ°ΤΫΦδΨύΈΣ![]()
ΫβΒΟ![]() Μρ
Μρ![]() ΘΜ
ΘΜ
ΔΎ»τ![]() Θ§‘ρBΓΔCΦδ”–œύΕ‘‘ΥΕ·Θ§ΗςΉ‘œύΕ‘ΒΊΟφΦθΥΌΒΫΥΌΕ»ΈΣ0Θ§Ε‘A”–
Θ§‘ρBΓΔCΦδ”–œύΕ‘‘ΥΕ·Θ§ΗςΉ‘œύΕ‘ΒΊΟφΦθΥΌΒΫΥΌΕ»ΈΣ0Θ§Ε‘A”–
![]()
Μ§ΩιAΆΘ÷Ι ±ΨύNΒψΒΡΥ°ΤΫΦδΨύΈΣ![]()
ΫβΒΟ: ![]() Μρ
Μρ![]()

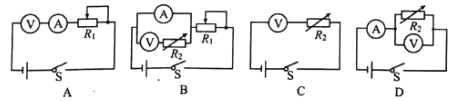
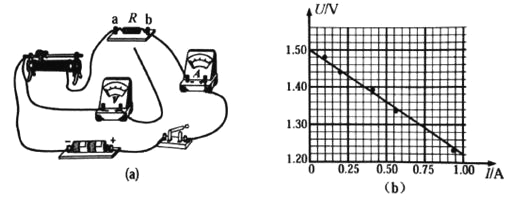
ΓΨΧβΡΩΓΩΡ≥–Θ Β―ι–ΓΉι…ηΦΤΝΥ»γœ¬ Β―ιά¥ΨΪ»Ζ≤βΕ®–Γ≥ΒΒΡΥ≤ ±ΥΌΕ»ΓΘ»γΆΦΥυ ΨΘ§‘Ύ«ψ–±ΒΦΙλΒΡA¥ΠΖ≈÷Ο“ΜΙβΒγΟ≈Θ§≤Δ ΙΤδ”κΦΤΥψΜζΝ§Ϋ”ΓΘ»Ο‘Ί”–«α÷ Β≤ΙβΤ§![]() ΩμΕ»ΈΣ
ΩμΕ»ΈΣ![]() ΒΡ–Γ≥Β¥”PΒψΨ≤÷Ιœ¬Μ§Θ§A¥ΠΒΡΙβΒγΟ≈ΜαΦ«¬Φœ¬Β≤ΙβΤ§Ψ≠ΙΐAΒψΥυΨ≠άζΒΡ ±Φδ
ΒΡ–Γ≥Β¥”PΒψΨ≤÷Ιœ¬Μ§Θ§A¥ΠΒΡΙβΒγΟ≈ΜαΦ«¬Φœ¬Β≤ΙβΤ§Ψ≠ΙΐAΒψΥυΨ≠άζΒΡ ±Φδ![]() ΗΡ”Ο≤ΜΆ§ΩμΕ»ΒΡΒ≤ΙβΤ§÷ΊΗ¥…œ ω Β―ιΘ§
ΗΡ”Ο≤ΜΆ§ΩμΕ»ΒΡΒ≤ΙβΤ§÷ΊΗ¥…œ ω Β―ιΘ§![]() ‘Ύ‘≠Β≤ΙβΤ§Μυ¥Γ…œΧυ…œΩμΕ»≤ΜΆ§ΚΎ÷ΫΤ§÷ΤΒΟ
‘Ύ‘≠Β≤ΙβΤ§Μυ¥Γ…œΧυ…œΩμΕ»≤ΜΆ§ΚΎ÷ΫΤ§÷ΤΒΟ![]() »ΜΚσ”ΟΙΪ Ϋ
»ΜΚσ”ΟΙΪ Ϋ![]() ΦΤΥψ≥ω≤ΜΆ§ΩμΕ»ΒΡΒ≤ΙβΤ§¥”AΒψΩΣ Φ‘ΎΗςΉ‘Β≤Ιβ ±Φδ
ΦΤΥψ≥ω≤ΜΆ§ΩμΕ»ΒΡΒ≤ΙβΤ§¥”AΒψΩΣ Φ‘ΎΗςΉ‘Β≤Ιβ ±Φδ![]() ΡΎΒΡΓΘΗΟ–ΓΉι Β―ι ΐΨί»γ±μ
ΡΎΒΡΓΘΗΟ–ΓΉι Β―ι ΐΨί»γ±μ
¥Έ ΐ | Β≤ΙβΤ§Β≤Ιβ ±Φδ | ΥΌΕ» |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
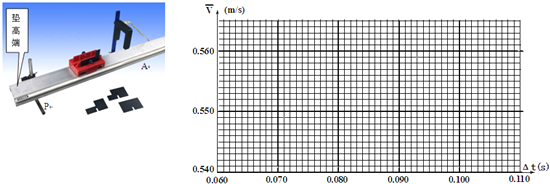
‘Ύ“‘…œ Β―ιΒΡΜυ¥Γ…œΘ§«κΦΧ–χΆξ≥…œ¬Ν– Β―ι»ΈΈώΘΚ
![]() ΗυΨί Β―ι ΐΨί‘Ύ
ΗυΨί Β―ι ΐΨί‘Ύ![]() ΆΦ…œΉς≥ωΗΟ Β―ιΆΦœΏ_____________ΓΘ
ΆΦ…œΉς≥ωΗΟ Β―ιΆΦœΏ_____________ΓΘ
![]() ΫαΚœ Β―ι‘≠άμΘ§ΆΤΒΦ≥ω
ΫαΚœ Β―ι‘≠άμΘ§ΆΤΒΦ≥ω![]() ΆΦœΏΥυ¬ζΉψΒΡΚ· ΐ Ϋ___________ΓΘ
ΆΦœΏΥυ¬ζΉψΒΡΚ· ΐ Ϋ___________ΓΘ
![]() ΗυΨί
ΗυΨί![]() ΆΦœΏΥυ¬ζΉψΒΡ
ΆΦœΏΥυ¬ζΉψΒΡ![]() Κ· ΐ ΫΘ§«σ≥ωΒ≤ΙβΤ§Ήν«ΑΕΥΨ≠ΙΐAΒψ ±ΒΡΥ≤ ±ΥΌΕ»
Κ· ΐ ΫΘ§«σ≥ωΒ≤ΙβΤ§Ήν«ΑΕΥΨ≠ΙΐAΒψ ±ΒΡΥ≤ ±ΥΌΕ»![]() =___________ΓΘ
=___________ΓΘ
![]() ΈΣΝΥΧαΗΏ Β―ιΨΪ»ΖΕ»Θ§ Β―ι≤ΌΉς÷–±Ί–κΉωΒΫΒΡ «______
ΈΣΝΥΧαΗΏ Β―ιΨΪ»ΖΕ»Θ§ Β―ι≤ΌΉς÷–±Ί–κΉωΒΫΒΡ «______
![]() ΗϋΜΜΒ≤ΙβΤ§ ±”Π ΙΤδ«Α―Ί Φ÷’¥Π”Ύ–Γ≥Β…œΒΡΆ§“ΜΈΜ÷Ο
ΗϋΜΜΒ≤ΙβΤ§ ±”Π ΙΤδ«Α―Ί Φ÷’¥Π”Ύ–Γ≥Β…œΒΡΆ§“ΜΈΜ÷Ο
![]() ΟΩ¥ΈΕΦ”Π¥”ΙλΒά…œΆ§“ΜΈΜ÷Ο”…Ψ≤÷Ι ΆΖ≈–Γ≥Β
ΟΩ¥ΈΕΦ”Π¥”ΙλΒά…œΆ§“ΜΈΜ÷Ο”…Ψ≤÷Ι ΆΖ≈–Γ≥Β
![]() Β―ιΩΣ Φ«Α±Ί–κΒς’ϊΙλΒά«ψΫ«Θ§ΤΫΚβΡΠ≤ΝΝΠ
Β―ιΩΣ Φ«Α±Ί–κΒς’ϊΙλΒά«ψΫ«Θ§ΤΫΚβΡΠ≤ΝΝΠ
![]() ΗϋΜΜΒΡΒ≤ΙβΤ§ΩμΕ»≤ΜΡήΙΐΩμΘ§ΩμΕ»‘Ϋ’≠Θ§
ΗϋΜΜΒΡΒ≤ΙβΤ§ΩμΕ»≤ΜΡήΙΐΩμΘ§ΩμΕ»‘Ϋ’≠Θ§![]() ‘Ϋ–ΓΘ§«σ≥ωΒΡ
‘Ϋ–ΓΘ§«σ≥ωΒΡ![]() ‘ΫΨΪ»ΖΓΘ
‘ΫΨΪ»ΖΓΘ