题目内容
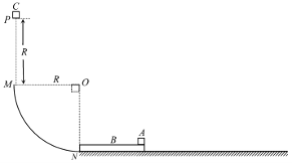
【题目】如图所示为质谱仪的示意图,在容器A中存在若干种电荷量相同而质量不同的带电粒子,它们可从容器A下方的小孔S1飘入电势差为U的加速电场,它们的初速度几乎为0,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上。若这些粒子中有两种电荷量均为q、质量分别为m1和m2的粒子(m1<m2)。
(1)分别求出两种粒子进入磁场时的速度v1、v2的大小;
(2)求这两种粒子在磁场中运动的轨道半径之比;
(3)求两种粒子打到照相底片上的位置间的距离。
【答案】(1)![]() 、
、![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (
(![]() -
-![]() )。
)。
【解析】
(1)带电粒子在电场中被加速,应用动能定理可以求出粒子的速度。
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的轨道半径,然后求出半径之比。
(3)两粒子在磁场中做圆周运动,求出其粒子轨道半径,然后求出两种粒子打到照相底片上的位置间的距离。
(1)经过加速电场,根据动能定理得:
对m1粒子:qU=![]() m1v12
m1v12
m1粒子进入磁场时的速度:![]() ,
,
对m2粒子有:qU=![]() m2v22,
m2v22,
m2粒子进入磁场时的速度:![]() ;
;
(2)在磁场中,洛仑兹力提供向心力,由牛顿第二定律得:qvB=m![]() ,
,
解得,粒子在磁场中运动的轨道半径:![]() ,
,
代入(1)结果,可得两粒子的轨道半径之比:R1:R2=![]() ;
;
(3)m1粒子的轨道半径:![]() ,
,
m2粒子的轨道半径: ![]() ,
,
两粒子打到照相底片上的位置相距:d=2R2-2R1,
解得,两粒子位置相距为:![]() ;
;

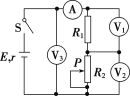
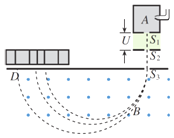
【题目】某同学用图甲所示电路来测绘小灯泡的伏安特性曲线,器材如下:
A.小灯泡(额定电压2.5V,额定电流0.25A)
B.电流表(0~0.6A)
C.电压表(0~3V)
D.滑动变阻器R1(0~10Ω)
E.滑动变阻器R2(0~1000Ω)
F.干电池(电动势为1.5V)两节
G.开关,导线若干
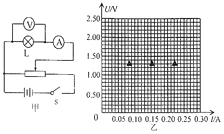
(1)滑动变阻器应选_____(选填器材前的代号);
(2)实验中得到的数据如下表所示,根据表中数据在乙图中作出小灯泡的U﹣I图象_________,由图象可知小灯泡的电阻随温度的升高而_____(选填“增大”、“减小”或“不变”)。
U/V | 0.20 | 0.40 | 0.60 | 1.00 | 1.40 | 1.80 | 2.00 | 2.20 |
I/A | 0.04 | 0.08 | 0.11 | 0.15 | 0.18 | 0.20 | 0.21 | 0.22 |
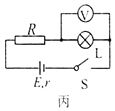
(3)某同学用一节干电池与阻值为5Ω的电阻R、小灯泡及电压表连接成图丙所示电路。闭合S后,电压表测得灯泡两端电压为0.8V,结合图乙图中图象求得小灯泡实际消耗的功率为_____W,干电池内阻为_____Ω.(结果均保留两位有效数字)