��Ŀ����
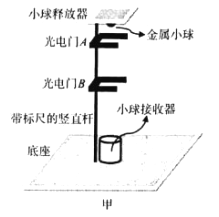
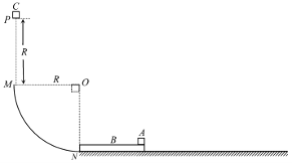
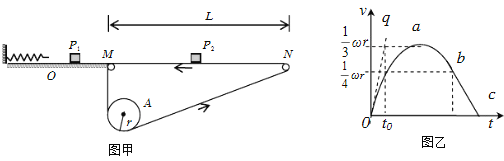
����Ŀ����ͼ�ף�ˮƽ��������һ�����ʵ�����Ȼ�쳤����˹̶���ǽ���ϣ��Ҷ�λ��O��![]() �����Ҷ�M��������װ�ã����ϱ����������ͬһˮƽ��
�����Ҷ�M��������װ�ã����ϱ����������ͬһˮƽ��![]() ����װ���ڰ뾶Ϊr�����ٶ�Ϊ
����װ���ڰ뾶Ϊr�����ٶ�Ϊ![]() ����A��������ͼʾ����
����A��������ͼʾ����![]() �ڵ����ȷ�Χ�ڣ���С���
�ڵ����ȷ�Χ�ڣ���С���![]() ����ѹ�����ɵ�ѹ����Ϊxʱ�ͷţ�
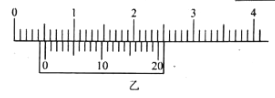
����ѹ�����ɵ�ѹ����Ϊxʱ�ͷţ�![]() ����M��ʱ��ֹ�����ٶ�ͼ����ͼ����ʾ
����M��ʱ��ֹ�����ٶ�ͼ����ͼ����ʾ![]() ����0qΪͼ����ԭ������ߣ�bc��Ϊֱ��
����0qΪͼ����ԭ������ߣ�bc��Ϊֱ��![]() ֮�����
֮�����![]() �ڴ���װ������M����Ϊl��λ�þ�ֹ�ͷţ�
�ڴ���װ������M����Ϊl��λ�þ�ֹ�ͷţ�![]() ��
��![]() ��ײ��ճ��һ��
��ײ��ճ��һ��![]() ��֪
��֪![]() ��
��![]() ������Ϊm���봫��װ�á�ˮƽ����Ķ�Ħ��������Ϊ
������Ϊm���봫��װ�á�ˮƽ����Ķ�Ħ��������Ϊ![]() ��M��N����Ϊ
��M��N����Ϊ![]() ���������ٶ�Ϊg��
���������ٶ�Ϊg��
![]() �ɵľ���ϵ��k�Լ�O��M�ľ���s��
�ɵľ���ϵ��k�Լ�O��M�ľ���s��
![]() Ҫʹ
Ҫʹ![]() ��
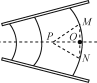
��![]() ��ײ��Ľ����P�ܻص�O�㣬��l��ȡֵ��Χ�Լ�P�ص�O��ʱ���ٶȴ�Сv��l�Ĺ�ϵ����ʽ��
��ײ��Ľ����P�ܻص�O�㣬��l��ȡֵ��Χ�Լ�P�ص�O��ʱ���ٶȴ�Сv��l�Ĺ�ϵ����ʽ��
���𰸡�![]() ��
��![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��������
Ӧ��ţ�ٵڶ��������ȱ����˶����ٶ�λ�ƹ�ʽ�������⣻�ɶ����غ㶨�����ȱ����˶����ٶ�λ�ƹ�ʽ�������⡣
![]() ��ͼ��֪�����ͷŵ���ʱ��
��ͼ��֪�����ͷŵ���ʱ��![]() ���еļ��ٶ�Ϊ��
���еļ��ٶ�Ϊ��![]()
�ɺ��˶��ɵô�ʱ���ɵ���Ϊ��![]()
��ţ�ٵڶ����ɵã�![]()
��õ��ɵľ���ϵ��Ϊ��![]()
��ͼ�ң�![]() �뿪��
�뿪��![]() ��ʱ���ٶ�Ϊ��
��ʱ���ٶ�Ϊ��![]()
֮��![]() �����ٶ�Ϊ��
�����ٶ�Ϊ��![]() ����
����![]() ����ֱ���˶���Mʱ�ٶ�Ϊ�㣬���ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�ã�
����ֱ���˶���Mʱ�ٶ�Ϊ�㣬���ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�ã�![]() ���O��M����Ϊ��
���O��M������![]()
![]() ��
��![]() ��ǰ˲���ٶ�Ϊ
��ǰ˲���ٶ�Ϊ![]() ����������P���ٶ�Ϊ
����������P���ٶ�Ϊ![]() ����ײǰ�����غ㣬��
����ײǰ�����غ㣬��![]() �ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
�ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�![]() ����
����![]() ��
��![]() �����P���ڵ����������ȼ��ٻص�O��ʱ�ٶ�Ϊv�����ٶ�λ�ƹ�ʽ�ã�
�����P���ڵ����������ȼ��ٻص�O��ʱ�ٶ�Ϊv�����ٶ�λ�ƹ�ʽ�ã�![]() ��
��![]() �ڴ���װ����һֱ���ٵ�M�㣬���У�
�ڴ���װ����һֱ���ٵ�M�㣬���У�![]()
������ã�![]()
Ҫʹ�����P�ܻص�O�㣬����![]() ����
����![]()
��![]() �ڴ���װ����һֱ���ٵ�M��ʱ�պ��봫��װ�ôﵽ��ͬ�ٶȣ�����
�ڴ���װ����һֱ���ٵ�M��ʱ�պ��봫��װ�ôﵽ��ͬ�ٶȣ�����![]()
��ã�![]()
i����![]() ʱ��
ʱ��![]() �ڴ���װ����һֱ���٣������ս����P�ܻص�O�㣬�ص�O��ʱ���ٶ�Ϊ��
�ڴ���װ����һֱ���٣������ս����P�ܻص�O�㣬�ص�O��ʱ���ٶ�Ϊ��![]()
ii����![]() ʱ��
ʱ��![]() �ڴ���װ�����ȼ��ٺ����٣���
�ڴ���װ�����ȼ��ٺ����٣���![]() ��ǰ˲���ٶ�ʼ��Ϊ
��ǰ˲���ٶ�ʼ��Ϊ![]() ��������ʽ�ã�
��������ʽ�ã�![]()