题目内容
【题目】如图所示,倾角为![]() 的传送带以速度v1=2m/s顺时针匀速转动。将一物块以v2=8m/s的速度从传送带的底端滑上传送带。已知小物块与传送带间的动摩擦因数
的传送带以速度v1=2m/s顺时针匀速转动。将一物块以v2=8m/s的速度从传送带的底端滑上传送带。已知小物块与传送带间的动摩擦因数![]() ,传送带足够长,取
,传送带足够长,取![]() , g=10m/s2,下列说法正确的是
, g=10m/s2,下列说法正确的是
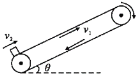
A.小物块向上运动过程中的加速度大小为10m/s2
B.小物块向上运动的时间为1. 6s
C.小物块向上滑行的最远距离为3m
D.小物块最终将随传送带一起向上匀速运动
【答案】B
【解析】
ABD.由于物块的速度大于传送带的速度,所以物块相对传送带向上运动,物块受重力和沿斜面向下的滑动摩擦力,沿斜面方向有根据牛顿第二定律:mgsinθ+μmgcosθ=ma1,代入数据解得:
a1=10m/s2
方向沿斜面向下。
设物体减速到传送带速度需要的时间为t1,有
![]()
由于物体所受重力沿斜面方向的分力大于滑动摩擦力,因此物体相对传送带向下运动,受到的滑动摩擦力沿斜面向上,沿斜面方向根据牛顿第二定律有:mgsinθ-μmgsosθ=ma2,代入数据解得:
a2=2m/s2
方向沿斜面向下;最后减速到速度为零的时间为:
![]()
故小物块向上运动的时间为1.6s。故B正确,AD错误。
C.小物块向上滑行的最远距离为:
![]()
故C错误。
故选B。

练习册系列答案
相关题目