题目内容
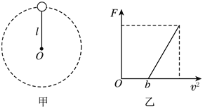
【题目】如图所示,绝缘光滑圆形导轨固定于竖直面内,半径R=0.4m。空间存在与轨道平面平行的匀强电场。带电小球沿轨道内侧做完整的圆周运动,小球动能最大的位置在A点,圆心O与A点的连线与竖直方向的夹角为θ。在A点时小球对轨道的压力FN=120N,运动过程中小球的最大动能比最小动能多16J。当小球在动能最小位置时突然撤去轨道,并保持其他条件都不变,则经![]() s时间后小球动能与在A点时的动能相等。(不计空气阻力,g取10m/s2,小球所带电荷量保持不变)则下列说法正确的是( )
s时间后小球动能与在A点时的动能相等。(不计空气阻力,g取10m/s2,小球所带电荷量保持不变)则下列说法正确的是( )

A.小球在轨道内运动时对轨道的最小压力等于小球重力
B.小球在轨道内运动的最小动能为4J
C.小球的质量为1kg
D.若θ=60°,则小球受到的电场力为![]() N
N
【答案】BC
【解析】
将重力场和电场合成为等效场,其合力将沿OA方向,在A点由牛顿第二定律:
![]()
而在A点由牛顿第三定律:
![]()
小球从等效最低点到等效最高点,由动能定理:
![]()
有:
![]()
B.联立各式解得:
![]()
![]()
故B项正确。
A.小球在等效最高点时对轨道的压力最小,由牛顿第二定律:
![]()
解得:
![]()
故小球在轨道内运动时对轨道的最小压力等于零,A项错误;
C.小球在动能最小位置时突然撤去轨道,并保持其他条件都不变,则小球做类平抛运动,经![]() s时间后沿等效重力的方向的速度为:
s时间后沿等效重力的方向的速度为:
![]()
合速度为
![]()
动能为:
![]()
联立解得:
![]()
![]()
故C项正确;
D.根据所求结果![]() ,重力
,重力![]() ,两者的夹角为θ=60°,则电场力为:
,两者的夹角为θ=60°,则电场力为:
![]()
故D项错误。

练习册系列答案
相关题目