题目内容
【题目】CD、EF是水平放置的电阻可忽略的光滑平行金属导轨,两导轨距离水平地面高度为H,导轨间距离为L,在水平导轨区域存在磁感强度方向垂直导轨平面向上的有界匀强磁场(磁场区域为CPQE),磁感应强度大小为B,如图所示,导轨左端与一弯曲的光滑轨道平滑连接,弯曲的光滑轨道的上端接有一电阻R,将一阻值也为R的导体棒从弯曲轨道上距离水平金属导轨高度h处由静止释放,导体棒最终通过磁场区域落在水平地面上距离水平导轨最右端水平距离x处.已知导体棒与导轨始终接触良好,重力加速度为g,求: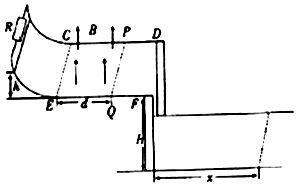
(1)电阻R中的最大电流和整个电流中产生的焦耳热;
(2)磁场区域的长度d.
【答案】
(1)解:由题意可知,导体棒刚进入磁场的瞬间速度最大,产生的感应电动势最大,感应电流最大,
由机械能守恒定律有 ![]()
解得 ![]()
由法拉第电磁感应定律得E=BLv1
由闭合电路欧姆定律得 ![]() ,
,
联立解得 ![]()
由平抛运动规律可得 ![]() ,
, ![]() ,
,
解得 ![]()
由能量守恒定律可知整个电路中产生的焦耳热为 ![]() ;
;
答:电阻R中的最大电流为 ![]() ,整个电流中产生的焦耳热为
,整个电流中产生的焦耳热为 ![]() ;
;
(2)导体棒通过磁场区域时在安培力作用下做变速运动.由牛顿第二定律,BIL=ma,
![]() ,
,
![]() ,
,
联立解得 ![]()
两边求和 ![]()
联立解得 ![]() .
.
答:磁场区域的长度为 ![]() .
.
【解析】(1)在进入磁场之前,导体棒的运动,满足机械能守恒。根据机械能守恒定律求出速度,切割磁感线的过程中,根据法拉第电磁定律以及闭合电路欧姆定律,再结合平抛运动的规律以及能量守恒定律综合列式求解。
(2)利用牛顿第二运动定律以及加速度的定义式,求出导体棒的加速度与安培力的关系,利用微元法,求解。
【考点精析】解答此题的关键在于理解电磁感应与电路的相关知识,掌握用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解,以及对电磁感应与力学的理解,了解用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解.