��Ŀ����
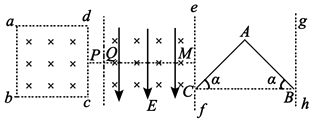
����Ŀ����ͼ��ʾ����������ϸ�ߵ�һ��˩��O�㡢��һ�˷ֱ�̶���¥���ڵ���б�컨���ϵ�a���b�㣬һ����Ϊm������Pͨ������ΪL������ϸ�߹̶���O�㣬ϵͳ��ֹ��Oaˮƽ��Ob����ֱ�����һ���нǣ����ڶ�����ʩ��һ��ˮƽ���ҵ�����F��ʹ���ﻺ���ƶ�����OP��ϸ��ת��60�㣬�˹�������������W���������ж���ȷ���ǣ�������
A.Oa�ϵ�����F1��������Ob�ϵ�����F2һ������
B.Oa�ϵ�����F1���ܲ��䣬Ob�ϵ�����F2��������
C.W= ![]() mgL������������˲ʱ����һֱ����
mgL������������˲ʱ����һֱ����
D.W= ![]() FL������������˲ʱ������������С
FL������������˲ʱ������������С
���𰸡�A,C
���������⣺A����ʼʱ�����ܵ����������ӵ��������������ӵ��������������������
�������ʩ��һ��ˮƽ���ҵ���������OC����ֱ����֮�������Ϊ�ȣ���ͼ�����У� ![]()

ѡ��ڵ�O��Ϊ�о�������O���ܵ������������ô���ƽ��״̬��������ͼ��
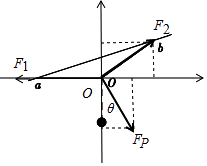
��ͼ��֪������ֱ����F2����ֱ����ķ���ʼ�յ���FPcos��=mg������F2�ķ���ʼ�ղ��䣬����F2ʼ�ղ��䣻
��ˮƽ����F1�Ĵ�С����F2��ˮƽ����ķ�����FP��ˮƽ��������ĺͣ�����FP��ˮƽ���������ȵ��������������F1������A�������⣬B���������⣻
CD���������֪������O������Բ���˶�����������������ֱ�뾶����ķ����ȴ�������������P=��mgsin�ȣ���v���������ݶ��ܶ�����֪W=mgL��1��cos60�㣩��C�������⡢D���������⣮
�ʴ�Ϊ��AC
��O�������Ϊ�о���������������������ݶ���ƽ���ж����ӵ�����������ʸ�������η�������������С�ı仯������ٽ�϶��ܶ������ʵĹ�ʽ�жϹ��ʵı仯�����

 ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�