题目内容
16.一颗小行星环绕太阳做匀速圆周运动的半径是地球公转半径的4倍,则这颗小行星的运转周期是( )| A. | 4年 | B. | 6年 | C. | 8年 | D. | 9年 |
分析 研究行星绕太阳做匀速圆周运动,根据万有引力提供向心力,列出等式表示出周期,
再根据地球与行星的轨道半径关系找出周期的关系.
解答 解:根据万有引力提供向心力得:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,
小行星环绕太阳做匀速圆周运动的半径是地球公转半径的4倍,所以这颗小行星的运转周期是8年,
故选:C.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行作比.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
6.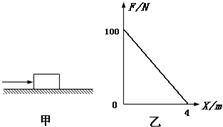 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示.已知物体与地面间的动摩擦因数为μ=0.5,g=10m/s2.下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示.已知物体与地面间的动摩擦因数为μ=0.5,g=10m/s2.下列说法正确的是( )
 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示.已知物体与地面间的动摩擦因数为μ=0.5,g=10m/s2.下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示.已知物体与地面间的动摩擦因数为μ=0.5,g=10m/s2.下列说法正确的是( )| A. | 物体先做加速运动,推力撤去时开始做减速运动 | |
| B. | 物体在水平面上运动的最大位移是12m | |
| C. | 物体在运动中的加速度先变小后不变 | |
| D. | 物体运动的最大速度为8m/s |
7.探月热方兴未艾,我国研制的月球卫星“嫦娥一号”、“嫦娥二号”均已发射升空,“嫦娥三号”于2013年发射升空.假设“嫦娥三号”在地球表面的重力为G1,在月球表面的重力为G2;地球与月球均视为球体,其半径分别为R1、R2;地球表面重力加速度为g.则( )
| A. | 月球表面的重力加速度为$\frac{g{G}_{1}}{{G}_{2}}$ | |
| B. | 月球与地球的质量之比为$\frac{{G}_{1}{{R}_{2}}^{2}}{{G}_{2}{{R}_{1}}^{2}}$ | |
| C. | 月球卫星与地球卫星分别绕月球表面附近与地球表面附近运行的速度之比为$\sqrt{\frac{{G}_{1}{R}_{2}}{{G}_{2}{R}_{1}}}$ | |
| D. | “嫦娥三号”环绕月球表面附近做匀速圆周运动的周期为$\sqrt{\frac{{G}_{1}{R}_{2}}{g{G}_{2}}}$ |
4.下列叙述中正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 当分子力表现为引力时,分子势能随分子间距离的增加而增加 | |
| C. | 对于一定质量的理想气体,温度升高时,压强可能减小 | |
| D. | 已知水的密度和水的摩尔质量,则可以计算出阿伏加德罗常数 | |
| E. | 扩散现象说明分子之间存在空隙,同时分子在永不停息地做无规则运动 |
11.”嫦娥三号”在近月点的速度为υ1,加速度为a1;在远月点的速度为υ2,加速度为a2,则有( )
| A. | υ1>υ2,a1>a2 | B. | υ1<υ2,a1<a2 | C. | υ1<υ2,a1>a2 | D. | υ1>υ2,a1<a2 |
6.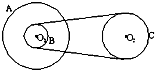 如图所示的皮带传动装置,A、B、C分别为轮缘上的三点,设皮带不打滑,A、C、B轮的半径比为3﹕2﹕1,则( )
如图所示的皮带传动装置,A、B、C分别为轮缘上的三点,设皮带不打滑,A、C、B轮的半径比为3﹕2﹕1,则( )
 如图所示的皮带传动装置,A、B、C分别为轮缘上的三点,设皮带不打滑,A、C、B轮的半径比为3﹕2﹕1,则( )
如图所示的皮带传动装置,A、B、C分别为轮缘上的三点,设皮带不打滑,A、C、B轮的半径比为3﹕2﹕1,则( )| A. | A、B两点的向心加速度之比为1:3 | |
| B. | B、C两点的向心加速度之比为1:2 | |
| C. | A、B、C三点的角速度之比ωA:ωB:ωC=1:1:2 | |
| D. | A、B、C三点的线速度之比vA:vB:vC=3:1:1 |
3.某著名极限运动员在美国新墨西哥州上空,从距地面高度约3.9万米的氦气球携带的太空舱上跳下,在最后几千英尺打开降落伞,并成功着陆.假设降落伞在最后的匀速竖直下降过程中遇到水平方向吹来的风,若风速越大,则降落伞( )
| A. | 下落的时间越短 | B. | 下落的时间越长 | C. | 落地时速度越小 | D. | 落地时速度越大 |
4.交流发电机在工作时的电动势e=EmSinωt.若将线圈匝数,线圈面积和角速度ω都提高到原来的两倍,其他条件不变,则电动势变为( )
| A. | e=8EmSinωt | B. | e=8EmSin2ωt | C. | e=4EmSin2ωt | D. | e=4EmSinωt |