题目内容
7.探月热方兴未艾,我国研制的月球卫星“嫦娥一号”、“嫦娥二号”均已发射升空,“嫦娥三号”于2013年发射升空.假设“嫦娥三号”在地球表面的重力为G1,在月球表面的重力为G2;地球与月球均视为球体,其半径分别为R1、R2;地球表面重力加速度为g.则( )| A. | 月球表面的重力加速度为$\frac{g{G}_{1}}{{G}_{2}}$ | |
| B. | 月球与地球的质量之比为$\frac{{G}_{1}{{R}_{2}}^{2}}{{G}_{2}{{R}_{1}}^{2}}$ | |
| C. | 月球卫星与地球卫星分别绕月球表面附近与地球表面附近运行的速度之比为$\sqrt{\frac{{G}_{1}{R}_{2}}{{G}_{2}{R}_{1}}}$ | |
| D. | “嫦娥三号”环绕月球表面附近做匀速圆周运动的周期为$\sqrt{\frac{{G}_{1}{R}_{2}}{g{G}_{2}}}$ |
分析 根据重力表达式G=mg表示出g进行比较,
忽略星球自转的影响,根据万有引力等于重力列出等式.
研究卫星在月球表面轨道上做匀速圆周运动,根据万有引力提供向心力,列出等式求解.
解答 解:A、该卫星在地球表面的重力为G1,在月球表面的重力为G2,
地球表面处的重力加速度为g,
根据重力表达式G=mg得:月球表面处的重力加速度为$\frac{g{G}_{2}}{{G}_{1}}$.故A错误.
B、忽略星球自转的影响,根据万有引力等于重力列出等式$\frac{GMm}{{R}^{2}}$=mg
M=$\frac{{gR}^{2}}{G}$
已知地球半径为R1,月球半径为R2,
所以月球的质量与地球的质量之比$\frac{{G}_{2}{{R}_{2}}^{2}}{{G}_{1}{{R}_{1}}^{2}}$,故B错误.
C、最大环绕速度v=$\sqrt{\frac{GM}{R}}$=$\sqrt{gR}$=$\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$,故C错误
D、研究卫星在月球表面轨道上做匀速圆周运动,根据万有引力提供向心力,列出等式$\frac{GMm}{{R}^{2}}$=m$\frac{{4π}^{2}R}{{T}^{2}}$
T=2π$\sqrt{\frac{{R}^{3}}{GM}}$①
而M=$\frac{{gR}^{2}}{G}$ ②
所以由①②得卫星在月球表面轨道上做匀速圆周运动的周期为2π$\sqrt{\frac{{G}_{1}{R}_{2}}{g{G}_{2}}}$,故D正确.
故选:D.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

 阅读快车系列答案
阅读快车系列答案 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球A、B分别处于竖直墙面和水平地面,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,并待两球重新达到平衡时,下列说法错误的是( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球A、B分别处于竖直墙面和水平地面,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,并待两球重新达到平衡时,下列说法错误的是( )| A. | 两小球之间库仑力减小 | |
| B. | 两小球之间电势能减小 | |
| C. | 竖直墙面对小球A的弹力减小 | |
| D. | 整个系统机械能增量等于水平推力F做功 |
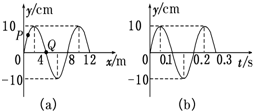 图(a)为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图(b)为质点Q的振动图象,下列说法正确的是( )
图(a)为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=4.0m处的质点;图(b)为质点Q的振动图象,下列说法正确的是( )| A. | 在t=0.10s时,质点Q向y轴正方向运动 | |
| B. | 在t=0.25s时,质点P的加速度方向与y轴正方向相反 | |
| C. | 从t=0.10s到t=0.25s,该波沿x轴负方向传播了6m | |
| D. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm |
 如图所示,用与竖直方向成α=30°的力F斜向上推住紧靠墙壁的物块B,将A置于B上,也紧靠墙壁,竖直墙粗糙,两物块保持静止状态.现增大推力F,物块A、B始终保持静止状态.下列说法正确的是( )
如图所示,用与竖直方向成α=30°的力F斜向上推住紧靠墙壁的物块B,将A置于B上,也紧靠墙壁,竖直墙粗糙,两物块保持静止状态.现增大推力F,物块A、B始终保持静止状态.下列说法正确的是( )| A. | 物块A受到的摩擦力增大 | B. | 物块B对物块A的作用力不变 | ||
| C. | 物块B受到的合外力变大 | D. | 物块B受到的摩擦力可能减小 |
| A. | 4年 | B. | 6年 | C. | 8年 | D. | 9年 |
| A. | 它是人造地球卫星环绕地球运转的最小速度 | |
| B. | 它是近地圆形轨道上人造卫星的运行速度 | |
| C. | 它是能使卫星进入近地轨道的最小发射速度 | |
| D. | 它是能使卫星进入近地轨道的最大发射速度 |
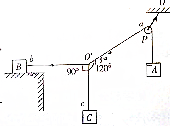 如图所示,物块A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O点,O点处安装一力传感器,质量为10kg的物块B放在粗糙的水平桌面上,bO′水平拉着物块B,CO′悬挂物块C,O′是三根线的结点,aO′、bO′与cO′夹角如图所示,细线、小滑轮的重力和细线与小滑轮间的摩擦力均可忽略,整个装置处于静止状态,若O点处安装的力传感器显示受到的拉力大小为F0=20$\sqrt{3}$N,物块B与水平桌面之间的动摩擦因数为0.2,重力加速度g=10m/s2,求:
如图所示,物块A被绕过小滑轮P的细线所悬挂,小滑轮P被一根细线系于天花板上的O点,O点处安装一力传感器,质量为10kg的物块B放在粗糙的水平桌面上,bO′水平拉着物块B,CO′悬挂物块C,O′是三根线的结点,aO′、bO′与cO′夹角如图所示,细线、小滑轮的重力和细线与小滑轮间的摩擦力均可忽略,整个装置处于静止状态,若O点处安装的力传感器显示受到的拉力大小为F0=20$\sqrt{3}$N,物块B与水平桌面之间的动摩擦因数为0.2,重力加速度g=10m/s2,求:


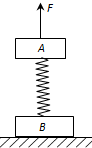 如图所示,一劲度系数K=800/md的轻质弹簧两端分别焊接着A,B两物体,MA=16kg,MB=8kg,直立于水平面而静止.现给物体A上加一个竖直向上的力F,使A由静止开始向上做匀加速运动,经 0.2s,B刚要离开地面,设整个过程弹簧都处于弹性限度内.(g取10 m/s2)求:
如图所示,一劲度系数K=800/md的轻质弹簧两端分别焊接着A,B两物体,MA=16kg,MB=8kg,直立于水平面而静止.现给物体A上加一个竖直向上的力F,使A由静止开始向上做匀加速运动,经 0.2s,B刚要离开地面,设整个过程弹簧都处于弹性限度内.(g取10 m/s2)求: