题目内容
【题目】在空间中几个点依次放置几个点电荷
，
，
，
，…，
，对于点
，其余
个点电荷在这一点上的电势和为
，若在这
个点上换上另个点电荷
，
，
，…，
，同理定义
（1）证明：
（2）利用（1）中结论，证明真空中一对导体电容器的电容值与这两个导体的带电量无关．（这对导体带等量异号电荷）
（3）利用（1）中的结论，求解如下问题：如图所示，正四面体
各面均为导体，但又彼此绝缘．已知带电后四个面的静电势分别为
、
、
和
，求四面体中心
点的电势
【答案】（1）证明见解析（2）证明见解析（3）
【解析】
（1）设
点对
点所产生的电势为
，同理易知点对点产生电势为
，而对于此二点系统，我们有
，即
所以，
，易知
为只与位置有关的参量．
又
（令
）
则
（只与位置有关）
所以，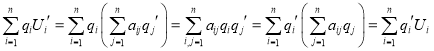
所以原式（格林互易定理）成立
（2）分别设两导体前后所带静电分别为
，
，其对应的电容分别为
、
则由（1）知，
（其中
，
为带时两导体电势）
同样
（其中
，
为带时两导体电势）
由（1）知二者相等，则
所以，
即与导体带电量多少无关．
（3）由题意，设四个面与中心
的电荷量分别为
、
、
、
、0
同时，四个面与中心的电势分别为
、
、
、
、
．
现将外面四个面接地，中心放一个电量为
的点电荷，中心电势为
，而四个面产生的感应电荷都相等，为
，则此时四个面与中心的电荷和电势分别为
、、、、；0、0、0、0、
由格林互易定理可得
即可得
练习册系列答案
相关题目
