题目内容
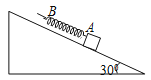
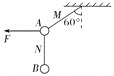
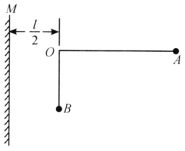
【题目】如图所示,竖直平面内有悬点![]() 和
和![]() ,
,![]() 上有一原长为0的弹性轻绳,弹性绳的劲度系数为
上有一原长为0的弹性轻绳,弹性绳的劲度系数为![]() ,悬于
,悬于![]() 点,另一端挂一质量为
点,另一端挂一质量为![]() 的小球
的小球![]() ,静止于
,静止于![]() 处,另有一个同样的弹性绳悬于
处,另有一个同样的弹性绳悬于![]() 点,和
点,和![]() 小球一样的小球
小球一样的小球![]() 系在绳的另一端.现将
系在绳的另一端.现将![]() 球拉至水平,且
球拉至水平,且![]() ,
,![]() 点左边
点左边![]() 处有一竖直的弹性墙
处有一竖直的弹性墙![]() .初始时可使
.初始时可使![]() 具有竖直方向的速度
具有竖直方向的速度![]() ,且
,且![]() 能击中
能击中![]() ,求速度
,求速度![]() .(绳与绳之间不会相缠绕,
.(绳与绳之间不会相缠绕,![]() 球悬绳不会与
球悬绳不会与![]() “相碰”)
“相碰”)
【答案】![]()
【解析】
首先建立如图所示的坐标系.
依题意,质点![]() 的平衡位置在
的平衡位置在![]() 点.不难证明,质点
点.不难证明,质点![]() 在
在![]() 方向与
方向与![]() 方向上的运动都是简谐振动,且周期相同.
方向上的运动都是简谐振动,且周期相同.
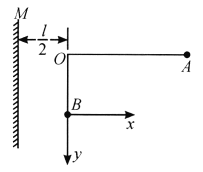
设![]() 的质量为
的质量为![]() ,则角频率为
,则角频率为![]() ,有
,有
![]()
![]()
(1)由题意可知,当![]() ,
,![]() 时,有
时,有
![]() ,
,![]() ,
,![]() ,
,![]()
即![]() ,
,![]()
显然,当![]() 时,有
时,有![]() ,
,![]() ,即
,即![]() 过
过![]() 点,符合题意
点,符合题意
(2)若![]() ,
,![]() (方向向下)时,先讨论
(方向向下)时,先讨论![]() 在
在![]() 方向上的运动
方向上的运动
在未撞墙时的运动仍然是:![]() .而撞墙后的运动仍然是简谐振动,同时,其运动与撞前对称
.而撞墙后的运动仍然是简谐振动,同时,其运动与撞前对称
从开始至![]() 处需时
处需时![]()
从![]() 至撞墙
至撞墙![]() 处需时
处需时![]()
由上述条件,可知![]() 经过
经过![]() 处的时间
处的时间![]() 为
为![]()
![]() ,
,
![]()
![]()
![]()
…
![]()
![]()
所以,![]()
再讨论![]() 在
在![]() 方向上的运动.
方向上的运动.
由![]() 知
知![]()
将![]() ,
,![]() ,
,![]() 代入,得
代入,得![]() ,
,![]()
解得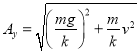 ,
,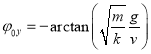
令![]() ,则要求
,则要求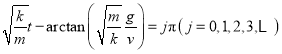
即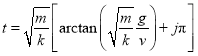
若![]() 能击中
能击中![]() 球,即
球,即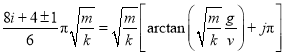
解得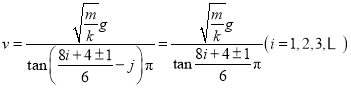
所以,![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目