题目内容
【题目】如图所示，竖直面内半径为R的四分之一圆周轨道AB固定在水平面上，轨道两端A、B在同一水不面上，以A点为坐标原点，建立竖直面内的直角坐标系，y轴沿竖直方向，坐标平面和圆弧轨道在同一竖直面内，在坐标面上第一象限内的P(
)点水平向左抛出一个小球，结果小球恰好能从A点无碰撞地进人圆弧轨道，不计空气阻力和小球大小，重力加速度为g。 求：
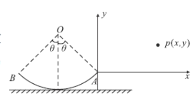
（1）小球抛出点P的坐标满足的条件；
（2）抛出点位置满足（1)问中的小球被抛出后，到达圆弧轨道的最低点时，对轨道的压力为其重力的5倍，求该小球抛出的初速度大小。
【答案】（1）
（2）
【解析】
(1)由于圆弧轨道为四分之一个圆弧，因此
从
点向左水平抛出的小球恰好能从
点无碰撞地进入园弧轨道，则小球在点的速度与水平方向的夹角为
，则有：
即
(2)设小球在圆弧轨道的最底点时速度大小为
，由题意可知：
解得：
设小球抛出的初速度大小为
，则小球在点的速度大小为
从点到轨道最低点，根据机械能守恒定律有：
解得：
练习册系列答案
相关题目
