��Ŀ����
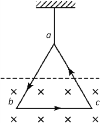
����Ŀ���������ͬ������ʱ���Ƚ����Ƿ���������Բ���1��Ȼ���ʹ������Բ���2���У�����ٴε�𣬽���������ͬ��Բ���3�����1��2������Q�㣬���2��3������P�㣬��ͼ��ʾ��������˵����ȷ������ ��
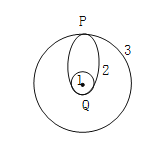
A. Ҫ��������Բ���1����Բ���3����Ҫ����Բ���2�Ľ��ص�Q��Զ�ص�P�ֱ������һ��
B. ����������Բ���1����Բ���3�����������Σ���������Բ���3�����������ٶ�Ҫ������Բ���1���������е��ٶ�
C. ��������Բ���2�ϵĽ��ص�Q���ٶ�һ������7.9km/s������Զ�ص�P���ٶ�һ��С��7.9km/s
D. ��������Բ���2�Ͼ���P��ʱ�ļ��ٶȵ�������Բ���3�Ͼ���P��ʱ�ļ��ٶ�
���𰸡�ACD
��������
�����1�����2�����Q�����������˶�����������٣������ڹ��2 ��P���������˶�������������������������������ٴμ��ٲ��ܱ�쵽���3������A��ȷ�����������䱻�������Σ������ڿ˷������������ٶȻ��С�����ٶȹ�ʽ![]() ��֪�����3�������ٶ�С�ڹ��1�������ٶȣ���B������������Բ���1���ٶ�Ϊ7.9km/s����������Բ���2�ϵĽ��ص�Q��Ҫ�������˶���������ٶ�һ������7.9km/s������Զ�ص�P���뾶���ڵ���뾶�����ٶ�һ��С��7.9km/s����C��ȷ������ţ�ٵڶ����ɺ������������ɵã�
��֪�����3�������ٶ�С�ڹ��1�������ٶȣ���B������������Բ���1���ٶ�Ϊ7.9km/s����������Բ���2�ϵĽ��ص�Q��Ҫ�������˶���������ٶ�һ������7.9km/s������Զ�ص�P���뾶���ڵ���뾶�����ٶ�һ��С��7.9km/s����C��ȷ������ţ�ٵڶ����ɺ������������ɵã�![]() �����������ڹ��2�Ͼ���Q��ļ��ٶȵ����ڹ��1�Ͼ���Q��ļ��ٶȣ���D��ȷ����������ѡB��
�����������ڹ��2�Ͼ���Q��ļ��ٶȵ����ڹ��1�Ͼ���Q��ļ��ٶȣ���D��ȷ����������ѡB��

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�