��Ŀ����
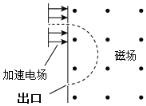
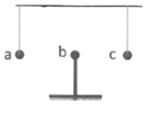
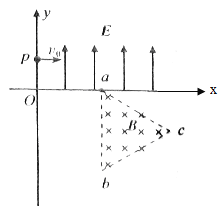
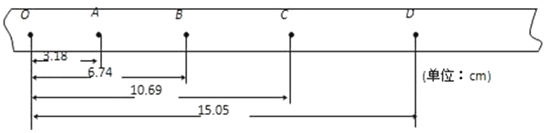
����Ŀ����ͼ��ʾ��������abcd�������д�ֱ��ֽ���������ǿ�ų���һ�������Բ�ͬ�����ʴ�a����ab���������ǿ�ų��У����������������ж���ȷ���ǣ�������

A. ��c������ĵ������d������ĵ�������֮��Ϊ1��2
B. ��bc���е�����ĵ��ӱȴ�cd���е�����ĵ����˶�����С
C. ���д�cd������ĵ����ڴų����˶�ʱ�䶼��ͬ
D. ���д�ad������ĵ����ڴų����˶�ʱ�䶼��ͬ
���𰸡�D
��������
���������ڴų�����Բ���˶��������������ṩ�����������ɼ���֪ʶ�ɷֱ���ô�c���d��ɳ������ӵĹ켣�뾶������ţ�ٵڶ����ɺ���������ʽ����������ӵ����ʣ������������֮�ȣ���ת���ĽǶȿɱȽ��˶�ʱ��֮�ȡ�
������ڴų����˶��Ĺ켣�뾶Ϊr���������������ṩ���������ã�qvB=m![]() ����ã�
����ã�![]() ���ɼ���v��r��
���ɼ���v��r��
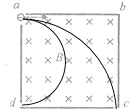
��ų��߳�ΪL����ͼ��ʾ�����Ӵ�c���뿪�ų�ʱ����켣�뾶Ϊ rc=L����d���뿪�ų��ĵ��ӣ���켣�뾶Ϊrd=![]() L����ã�vc��vd=2��l����A����bc���е�����ĵ��ӵ���ת�뾶�ȴ�cd���е�����ĵ�����ת�뾶�ϴ����bc���е�����ĵ��ӱȴ�cd���е�����ĵ����˶����ʴ�B���������Ӵ�cd����������������ų�ʱ������Խ����뾶Խ����ת����Բ�Ľ�ԽС�����ڴų��е��˶�ʱ���Խ�̣���C���������Ӵ�ad�������������ڴų���ת����Բ�ĽǶ���ȣ�����180���������ڴų��е��˶�ʱ����ȣ�����ӵ������أ���D��ȷ����ѡD��
L����ã�vc��vd=2��l����A����bc���е�����ĵ��ӵ���ת�뾶�ȴ�cd���е�����ĵ�����ת�뾶�ϴ����bc���е�����ĵ��ӱȴ�cd���е�����ĵ����˶����ʴ�B���������Ӵ�cd����������������ų�ʱ������Խ����뾶Խ����ת����Բ�Ľ�ԽС�����ڴų��е��˶�ʱ���Խ�̣���C���������Ӵ�ad�������������ڴų���ת����Բ�ĽǶ���ȣ�����180���������ڴų��е��˶�ʱ����ȣ�����ӵ������أ���D��ȷ����ѡD��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�