题目内容
9.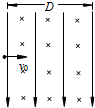 如图所示是一宽度为D=8cm的同时存在相互垂直的匀强电场和磁场的区域,一束带电粒子(不计重力)以速度v0射入时恰好不改变运动方向.若粒子射入时只有电场,可测得粒子束穿过电场时竖直方向上偏移h=3.2cm;若粒子射入时只有磁场,则离开磁场时偏离原方向的距离为多大?
如图所示是一宽度为D=8cm的同时存在相互垂直的匀强电场和磁场的区域,一束带电粒子(不计重力)以速度v0射入时恰好不改变运动方向.若粒子射入时只有电场,可测得粒子束穿过电场时竖直方向上偏移h=3.2cm;若粒子射入时只有磁场,则离开磁场时偏离原方向的距离为多大?
分析 若撤去磁场,粒子做类平抛运动,运用运动的分解,由水平位移和竖直位移研究电场强度与磁感应强度的关系.若撤去电场,粒子做匀速圆周运动,由牛顿第二定律求出半径,由几何知识求出穿过场区后的侧移.
解答 解:设带电粒子带电量为q,质量为m,电场强度为E,磁感应强度为B.
在电磁场中,带电粒子恰好没有偏转,说明其做匀速直线运动,则有:Bqv0=qE …①
只有电场时,做类平抛运动:
t=$\frac{d}{{v}_{0}}$…②
y1=$\frac{1}{2}$at2=$\frac{1}{2}$•$\frac{qE}{m}$•t2…③
只有磁场时,做匀速圆周运动,洛仑兹力提供向心力,Bqv0=m$\frac{{v}_{0}^{2}}{r}$…④
由①~④解得:r=$\frac{{d}^{2}}{2{y}_{1}}$=10cm>8cm,带电粒子从场区右则射出磁场
由几何关系得:y2=r-$\sqrt{{r}^{2}-{d}^{2}}$=4cm
答:带电粒子离开磁场时偏离原方向的距离y2为4cm.
点评 本题是速度选择器模型、电偏转和磁偏转的综合,要注意两种偏转研究方法的不同,电偏转运用运动的合成与分解,磁偏转画轨迹,根据几何关系结合洛仑兹力提供向心力列方程求解.

练习册系列答案
相关题目
20.如图甲所示,匝数为10匝的三角形线圈,其总电阻r=0.5Ω,外接一个阻值R=2.0Ω的电阻,在线圈内有垂直纸面向内的磁场,线圈内磁通量Φ随时间t变化的规律如图乙所示,下列说法正确的是( )
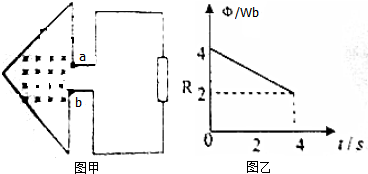

| A. | 电阻R两端电压为5V | B. | 电阻R上消耗的功率为8W | ||
| C. | 0~4秒内通过电阻R的电荷量为8C | D. | a点的电势低于b点的电势 |
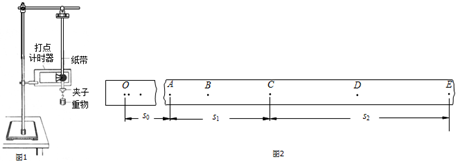
14.在验证机械能守恒定律的实验中,要验证的是重锤重力势能的减少量等于它的动能的增加,以下步骤中仅是实验中的一部分,在这些步骤中多余的或错误的有( )
| A. | 把打点计时器固定在铁架台上,并用导线把它和低压直流电源连接起来 | |
| B. | 把纸带的一端固定在重锤上,另一端穿过打点计时器的限位孔,把重锤提升到一定的高度 | |
| C. | 接通电源,释放纸带 | |
| D. | 用秒表测出重锤下落的时间 |
1.对于电动势和内阻确定的电源的路端电压,下列说法中正确的是(I、U、R分别表示干路电路电流、路端电压和外电阻)( )
| A. | U随着R的增大而减小 | B. | 当R=0时,U=E | ||
| C. | 当电路断开时,I=0,U=0 | D. | 当R增大时,U也会增大 |
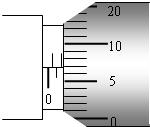
 在如图所示的电路中,电源的电动势E=3.6V,内电阻r=0.6Ω,外电路的电阻R=3.0Ω.闭合开关S.求:
在如图所示的电路中,电源的电动势E=3.6V,内电阻r=0.6Ω,外电路的电阻R=3.0Ω.闭合开关S.求: