Question

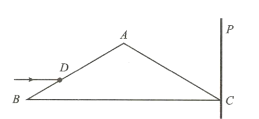
【题目】如图，等腰三角形ABC为真空中竖直面内的棱镜横截面，其底边BC水平，角B=30°,AB=L,P为过C点的竖直光屏。一束平行于BC边的光线射到AB边上D点，然后从AC边上F点（图中未画出）射出后在屏上产生光点。已知棱镜的折射率,BD=，真空中的光速为c,BC边只考虑一次反射。求：

(i)F点到A点的距离；

(ii)光线由D点传播到光屏P所用的时间。

Answer 1

【答案】(i)；(ii)

【解析】

（i）光路如答图4，设光在D点的入射角和折射角分别为i和r，在BC边的反射点为E。

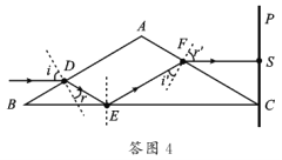
因入射光平行于BC，故i=60°，

由折射定律有

代入数据得r=30°，

因

∠BED=180°-∠B-90°-r=30°

故△BED为等腰三角形，DE=BD=，

由反射定律可知∠FEC=∠BED=30°，故ADEF为平行四边形，则有

EF=AD=AB-BD=

AF=DE=

（ii）设光点位置在S

光在棱镜中传播的距离为

x1=DE+EF=L

光在棱镜中传播的速度为

故光在棱镜中传播的时间为:

在F点光发生折射，易知:入射角，

由折射定律有

可得折射角，即FS∥BC，故

故光从F到S的时间为

解得时间