题目内容
14.8月16号我国成功的发射了“天空二号”,“天宫二号”是的运行轨道高度为393km.“天空一号”的运行轨道高度为350km,它们的运行轨道均视为圆周,则( )| A. | “天宫二号”比“天宫一号”速度大 | B. | “天宫二号”比“天宫一号”角速度大 | ||
| C. | “天宫二号”比“天宫一号”周期长 | D. | “天宫二号”比“天宫一号”加速度大 |
分析 “天空一号”和“天宫二号”都绕地球做匀速圆周运动,靠万有引力提供向心力,根据万有引力定律和牛顿第二定律比较线速度、周期、向心加速度的大小即可.
解答 解:A:“天空一号”和“天宫二号”绕地球做匀速圆周运动,靠万有引力提供向心力:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,即 v=$\sqrt{\frac{GM}{r}}$,“天宫二号”的轨道半径比“天空一号”大,则“天宫二号”比“天空一号”线速度小,故A错误;
B、万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=mrω2,解得ω=$\sqrt{\frac{GM}{{r}^{3}}}$,“天宫二号”的轨道半径比“天宫一号”大,则“天宫二号”比“天宫一号”角速度小,故B错误;
C、万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}r}{{T}^{2}}$解得:T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,天宫二号”的轨道半径比“天宫一号”大,则“天宫二号”比“天宫一号”周期长,故C正确;
D、根据万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=ma,解得a=$\frac{GM}{{r}^{2}}$,“天宫二号”的轨道半径比“天宫一号”大,则“天宫二号”比“天宫一号”加速度小,故D错误;
故选:C.
点评 解决本题的关键掌握天体运动中线速度、周期、向心加速度与轨道半径的关系,在实际考试中应注意结论的直接应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
5.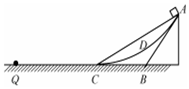 如图所示,斜面AB、AC的底端通过一小段圆弧与水平面相连,圆弧面ADC分别与斜面AB和水平面相切,小物块从A端分别由静止沿斜面AB,斜面AC,面ADC下滑.且都能经过水平面上的Q点,对应的速度分别为v1,v2,v3,已知小物块与水平面.斜面及圆弧面之间的动摩擦因数均相同.设小物块在斜面AB底端时的速度为v0,在斜面AC底端时的速度为vC,圆弧面底端的速度为vC′,不计物块在轨道接触处的机械能损失,则( )
如图所示,斜面AB、AC的底端通过一小段圆弧与水平面相连,圆弧面ADC分别与斜面AB和水平面相切,小物块从A端分别由静止沿斜面AB,斜面AC,面ADC下滑.且都能经过水平面上的Q点,对应的速度分别为v1,v2,v3,已知小物块与水平面.斜面及圆弧面之间的动摩擦因数均相同.设小物块在斜面AB底端时的速度为v0,在斜面AC底端时的速度为vC,圆弧面底端的速度为vC′,不计物块在轨道接触处的机械能损失,则( )
 如图所示,斜面AB、AC的底端通过一小段圆弧与水平面相连,圆弧面ADC分别与斜面AB和水平面相切,小物块从A端分别由静止沿斜面AB,斜面AC,面ADC下滑.且都能经过水平面上的Q点,对应的速度分别为v1,v2,v3,已知小物块与水平面.斜面及圆弧面之间的动摩擦因数均相同.设小物块在斜面AB底端时的速度为v0,在斜面AC底端时的速度为vC,圆弧面底端的速度为vC′,不计物块在轨道接触处的机械能损失,则( )
如图所示,斜面AB、AC的底端通过一小段圆弧与水平面相连,圆弧面ADC分别与斜面AB和水平面相切,小物块从A端分别由静止沿斜面AB,斜面AC,面ADC下滑.且都能经过水平面上的Q点,对应的速度分别为v1,v2,v3,已知小物块与水平面.斜面及圆弧面之间的动摩擦因数均相同.设小物块在斜面AB底端时的速度为v0,在斜面AC底端时的速度为vC,圆弧面底端的速度为vC′,不计物块在轨道接触处的机械能损失,则( )| A. | v1<v2 | B. | v2>v3 | C. | vC=vC′ | D. | vB=vC |
2.一个面积为S的矩形线圈在匀强磁场中做匀速转动,说法正确的是( )
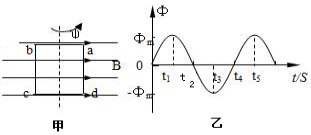

| A. | t1时刻线圈平面位于中性面位置 | B. | t2时刻ad的速度方向跟磁感线平行 | ||
| C. | t3时刻线圈平面与中性面重合 | D. | 在甲图位置电流方向发生改变 |
6.原子弹威力巨大,其主要原料有铀和钚,若有一铀原子核发生了如下的裂变反应:${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→A+B+2${\;}_{0}^{1}$n则A+B可能是( )
| A. | ${\;}_{54}^{140}Xe+{\;}_{38}^{94}Sr$ | B. | ${\;}_{54}^{140}Xe+{\;}_{36}^{93}Kr$ | ||
| C. | ${\;}_{56}^{141}Ba+{\;}_{36}^{92}Kr$ | D. | ${\;}_{56}^{141}Ba+{\;}_{38}^{93}Sr$ |
3. ${\;}_{92}^{238}$U是一种放射性元素,能够自发地进行一系列放射性衰变,如图所示,下列说法正确的是( )
${\;}_{92}^{238}$U是一种放射性元素,能够自发地进行一系列放射性衰变,如图所示,下列说法正确的是( )
 ${\;}_{92}^{238}$U是一种放射性元素,能够自发地进行一系列放射性衰变,如图所示,下列说法正确的是( )
${\;}_{92}^{238}$U是一种放射性元素,能够自发地进行一系列放射性衰变,如图所示,下列说法正确的是( )| A. | 图中a=84,b=206 | |
| B. | ${\;}_{82}^{206}$Pb比${\;}_{92}^{238}$U的比结合能大 | |
| C. | Y是β衰变,放出电子 | |
| D. | ${\;}_{82}^{206}$Pb的中子数比${\;}_{81}^{b}$Ti的多 |
4.下列叙述中正确的是( )
| A. | 已知水的摩尔质量和水分子的质量,可以计算出阿伏加德罗常数 | |
| B. | 布郎运动就是分子的无规则运动 | |
| C. | 对理想气体做功,内能不一定增加 | |
| D. | 分子间的相互作用力随着分子间距离的增大,一定先减小后增大 | |
| E. | 用活塞压缩汽缸内的理想气体,对气体做了3.0×105J的功,同时气体向外界放出1.5×105J的热量,则气体内能增加了1.5×105J |
 我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始,在无助力的情况下以加速度a=3.6m/s2匀加速滑下,到达B点时速度vB=24m/s,A与B的竖直高度差H=48m.为了改变运动员的运动方向,在助滑道与起跳台D点之间用一段弯曲滑道BCD衔接,B与C点的高度差h=5m,C与D点的高度差h′=4m,忽略BCD上的摩擦,g取10m/s2.求:
我国将于2022年举办冬奥会,跳台滑雪是其中最具观赏性的项目之一.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始,在无助力的情况下以加速度a=3.6m/s2匀加速滑下,到达B点时速度vB=24m/s,A与B的竖直高度差H=48m.为了改变运动员的运动方向,在助滑道与起跳台D点之间用一段弯曲滑道BCD衔接,B与C点的高度差h=5m,C与D点的高度差h′=4m,忽略BCD上的摩擦,g取10m/s2.求: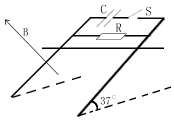 如图所示,在倾角为37度的斜面上有无限长的两条平行光滑金属导轨,导轨间距0.5m,导轨的上端接有阻值为R=0.8Ω的电阻和一电容为C=0.5F的电容器,磁感强度B=2T的匀强磁场,方向垂直于导轨平面向上,一质量为m=0.5kg,电阻r=0.2Ω的金属杆垂直导轨放置,开始时断开开关S,将杆由静止自由释放.(Sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,在倾角为37度的斜面上有无限长的两条平行光滑金属导轨,导轨间距0.5m,导轨的上端接有阻值为R=0.8Ω的电阻和一电容为C=0.5F的电容器,磁感强度B=2T的匀强磁场,方向垂直于导轨平面向上,一质量为m=0.5kg,电阻r=0.2Ω的金属杆垂直导轨放置,开始时断开开关S,将杆由静止自由释放.(Sin37°=0.6,cos37°=0.8,g=10m/s2)