题目内容
19.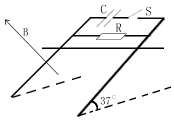 如图所示,在倾角为37度的斜面上有无限长的两条平行光滑金属导轨,导轨间距0.5m,导轨的上端接有阻值为R=0.8Ω的电阻和一电容为C=0.5F的电容器,磁感强度B=2T的匀强磁场,方向垂直于导轨平面向上,一质量为m=0.5kg,电阻r=0.2Ω的金属杆垂直导轨放置,开始时断开开关S,将杆由静止自由释放.(Sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,在倾角为37度的斜面上有无限长的两条平行光滑金属导轨,导轨间距0.5m,导轨的上端接有阻值为R=0.8Ω的电阻和一电容为C=0.5F的电容器,磁感强度B=2T的匀强磁场,方向垂直于导轨平面向上,一质量为m=0.5kg,电阻r=0.2Ω的金属杆垂直导轨放置,开始时断开开关S,将杆由静止自由释放.(Sin37°=0.6,cos37°=0.8,g=10m/s2)(1)求金属杆下滑的最大速度?
(2)若杆由静止下滑到速度最大的这段时间内通过杆的电荷量为2C,则在这段时间内电阻R上产生的热量?
(3)若在由静止释放杆的同时闭合开关,经过一段时间杆达到最大速度,这一过程中通过R的电荷量为5.76C,则这段时间为多少?
分析 (1)当杆下滑到最大速度时杆处于平衡状态,根据导体棒切割磁感线时感应电动势的计算公式、闭合电路欧姆定律、安培力的计算公式和物体平衡条件即可求出最大速度;
(2)根据某一过程中通过杆的电荷量计算公式q=$\frac{△Φ}{R+r}$可求解出杆从静止下滑到最大速度的过程中沿斜面下滑的距离x,根据能量守恒定律可求解出电路中产生的焦耳热进而可以求解出电阻R上产生的焦耳热;
(3)开关闭合后杆的最大速度不变,即杆到达最大速度后感应电动势E不变,结合通过电阻R的电荷量计算公式、电容器电容的定义式可求得通过杆的电荷量,由动量定理可求得时间t
解答 解:(1)设杆匀速运动时的速度为v,取杆为研究对象,则有:
E=BLv…①
I=$\frac{E}{R+r}$…②
F安=BIL…③
由平衡条件得:
mgsinθ-F安=0…④
由①②③④带入数据解得:v=3m/s
(2)设这段时间内,沿导轨方向导体棒移动的距离为x,则有:
$\overline{E}=\frac{△Φ}{△t}=\frac{BLx}{△t}$
${\overline{I}}_{1}=\frac{\overline{E}}{R+r}=\frac{BLx}{(R+r)△t}$
q1=$\overline{I}$1△t=$\frac{BLx}{R+r}$
所以:x=$\frac{{q}_{1}(R+r)}{BL}$=2m
设电路中产生的总热量为Q,由能量守恒定律得:
mgxsinθ=Q+$\frac{1}{2}$mv2
电阻R上产生的热量QR=$\frac{R}{R+r}$Q
解得:Q=3.75J、QR=3J
(3)开关闭合后杆的最大速度不变,即杆到达最大速度后感应电动势E不变,设这一过程所需时间为t,平均电流为$\overline{I}$,流过杆的总电荷量为Q,由动量定理得:
mgtsinθ-B$\overline{I}$Lt=mv
Q=$\overline{I}$t
Q=q+UC
解得:mgtsinθ=BLQ+mv
代入数据得:t=2.82s
答:(1)求金属杆下滑的最大速度为3m/s
(2)电阻R上产生的热量为3J
(3)这段时间为2.82s
点评 (1)本题考查了法拉第电磁感应定律、闭合电路欧姆定律、安培力的计算、能量守恒定律和动量定理
(2)根据能量守恒定律计算电路中产生的焦耳热是常用方法
(3)灵活引用动量定理是解决第三问的关键

 如图所示,实线表示在竖直平面内的电场线,电场线与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿虚线斜向上做直线运动,L与水平方向成β角,且α>β,则下列说法中正确的是( )
如图所示,实线表示在竖直平面内的电场线,电场线与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿虚线斜向上做直线运动,L与水平方向成β角,且α>β,则下列说法中正确的是( )| A. | 电场线方向一定斜向上 | B. | 液滴一定带负电 | ||
| C. | 液滴不一定做匀速直线运动 | D. | 液滴有可能做匀变速直线运动 |
| A. | 观察者静止,火车向他驶来 | |
| B. | 观察者静止,火车离他驶去 | |
| C. | 火车静止,观察者乘汽车向着火车运动 | |
| D. | 火车静止,观察者乘汽车远离火车运动 |
 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时零点,质点P的振动图象如图所示,已知O、P的平衡位置相距0.9m.以下判断正确的是( )
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时零点,质点P的振动图象如图所示,已知O、P的平衡位置相距0.9m.以下判断正确的是( )| A. | 波长为4m | |
| B. | 波源起振方向沿y轴正方向 | |
| C. | 波速大小为0.3m/s | |
| D. | 质点P的动能在t=4s时最小 | |
| E. | 质点P开始振动后的机械能是守恒的 |
| A. | “天宫二号”比“天宫一号”速度大 | B. | “天宫二号”比“天宫一号”角速度大 | ||
| C. | “天宫二号”比“天宫一号”周期长 | D. | “天宫二号”比“天宫一号”加速度大 |
| A. | J•J•汤姆逊发现不同物质发出的阴极射线的粒子比荷相同,这种粒子即电子 | |
| B. | β衰变时原子核会释放电子,说明电子也是原子核的组成部分 | |
| C. | 电子穿过晶体时会产生衍射图样,这证明了电子具有粒子性 | |
| D. | β射线是高速电子流,它的穿透能力比α射线和γ射线都弱 |
| A. | γ射线是电磁波,它的穿透能力最弱 | |
| B. | γ射线一般伴随着α或β射线产生,它的穿透能力最强 | |
| C. | α射线是原子核自发放射出的氦核流,它的穿透能力最强 | |
| D. | β射线是原子核外电子电离形成的电子流,它具有中等的穿透能力 |
 如图所示,横截面为直角三角形的斜劈P,靠在粗糙的竖直墙面上,力F通过球心水平作用在光滑球Q上,系统处于静止状态.当力F增大时,系统仍保持静止,下列说法正确的是( )
如图所示,横截面为直角三角形的斜劈P,靠在粗糙的竖直墙面上,力F通过球心水平作用在光滑球Q上,系统处于静止状态.当力F增大时,系统仍保持静止,下列说法正确的是( )| A. | 斜劈P所受合外力增大 | B. | 球Q对地面的压力不变 | ||
| C. | 墙面对斜劈P的摩擦力增大 | D. | 斜劈P对竖直墙壁的压力增大 |
| A. | 中子与质子结合成氘核的过程中需要吸收能量 | |
| B. | 一束光照射到某种金属上不能发生光电效应,是因为这束光的光强太小 | |
| C. | 依据玻尔理论,氢原子从低能级向高能级跃迁时,电子的动能将减小 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 |