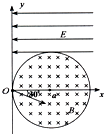
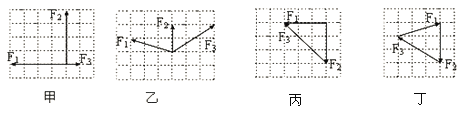
��Ŀ����
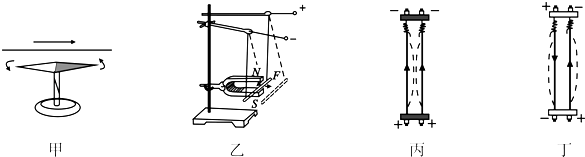
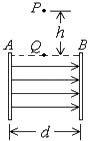
����Ŀ��Ϊ��̽�������ٶ������������Ĺ�ϵ������ˮƽ�̶��ij�ľ���ϣ�С��������A��B�ֱ�̽���˼��ٶ����������ı仯�Ĺ�ϵ��ʵ��װ����ͼ����ʾ������ʱ����ֽ��ͼ��δ��������ʵ�������С���ò�ͬ������P�ֱ���ڹ⻬�����ʶ������ϣ�ʹƽ���ڳ�ľ���ϸ��������ľ���ϵ�����A��B��ʵ���������ݴ�����
��1��Ϊ�˲������ɳӵľ���ϵ����С����������ʵ�飺�ڵ��ɳ��¶˹�һ��50g�Ĺ���ʱ��ָ��ʾ��ΪL1=3.50cm��������50g����ʱ��ָ��ʾ��ΪL2=5.10cm��gȡ9.8m/s2 �� �õ��ɳӵľ���ϵ��ΪN/m����������λ��Ч���֣�
��2��С�����ݼ�ͼ��ʵ�鷽���õ�������A��B�ļ��ٶ�a�����ʵ��ɳӵ���F�Ĺ�ϵͼ��ֱ���ͼ���е�A��B��ʾ��С����ϸ������ͼ���������߲��غϵ�ԭ�ó����ۣ�����������������ȣ���mAmB������ڡ���С�ڡ�������������ľ��֮�䶯Ħ��������A��B������ڡ������ڡ���С�ڡ�����
��3������ѡ�����ڼ�ͼ��ʾ��ʵ�鷽��������˵����ȷ����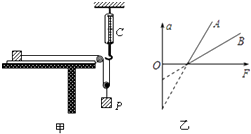
A.�������ж����ֵij�ľ������ʵ���ߣ�����ʹ��ͼ�е�ͼ�߹�ԭ��O
B.ʵ��ʱӦ�Ƚ�ͨ����ʱ����Դ���ͷ�����
C.ʵ��������P����������ԶС�����������
D.ʵ���е��ɳӵĶ���ʼ��Ϊ����P��������һ�룮
���𰸡�
��1��30.6
��2����,����
��3��A,B
���������⣺��1���赯�ɳ�ԭ��Ϊl������ƽ�����������˶��ɿ�֪��
mg=k��L1��l��
2mg=k��L2��l��
��ã�k=30.6 N/m��2������ٶȴ�СΪa����ţ�ٵڶ�������F����mg=ma���ɵã�a= ![]()
����a��Fͼ��б�ʾ���ֵk= ![]() ��֪��B��б�ʴ���A��б�ʣ���
��֪��B��б�ʴ���A��б�ʣ��� ![]() ������mA��mB��
������mA��mB��
�ٸ�������ؾ��С���ڦ�g��֪������A�Ľؾ����B�Ľؾ࣬���Ԧ�A����B����3��A���������ж����ֵij�ľ������ʵ���ߣ���ƽ��Ħ��������a��F��ͼ�߹�ԭ��O����A��ȷ��
B��ʵ��Ҫ��Ӧ�Ƚ�ͨ��Դ���ͷ�ֽ������B��ȷ��
C�����ڶ����������ʹ⻬�Ļ��֣��������Ӷ����������һ�����ڵ��ɳӵĶ�����������P������С��ֱ�ӹ�ϵ������C����
������P���������ٶ�Ϊaʱ��Ӧ��mg��2F=ma���ɵ�F= ![]() ������ֻ�е�a=0ʱ��F�ŵ���
������ֻ�е�a=0ʱ��F�ŵ��� ![]() ������D����
������D����
��ѡ��AB
���Դ��ǣ���1��30.6����2��С�ڣ����ڣ���3��AB

 ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�