题目内容
【题目】如图所示,在xoy坐标系内存在一个以(a,0)为圆心、半径为a的圆形磁场区域,方向垂直纸面向里,磁感应强度大小为B.另在y轴右侧有一方向向左的匀强电场,电场强度大小为E,分布于y≥a的范围内.O点为质子源,其出射质子的速度大小相等、方向各异,但质子的运动轨迹均在纸面内.已知质子在磁场中的偏转半径也为a,设质子的质量为m、电量为e,重力及阻力忽略不计.求: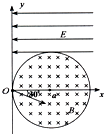
(1)出射速度沿x轴正方向的质子,到达y轴所用的时间;
(2)出射速度与x轴正方向成30°角(如图中所示)的质子,到达y轴时的位置;
(3)质子到达y轴的位置坐标的范围.
【答案】
(1)解:质子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力得:
evB= ![]()
即:v= ![]()
出射速度沿x轴正方向的质子,经 ![]() 圆弧后以速度v垂直于电场方向进入电场,在磁场中运动的时间为:
圆弧后以速度v垂直于电场方向进入电场,在磁场中运动的时间为:
t1= ![]() =
= ![]() =
= ![]()
质子进入电场后做类平抛运动,沿电场方向运动a后到达y轴,由匀变速直线运动规律有:
a= ![]()
即: ![]()
故所求时间为:t=t1+t2= ![]() +
+ ![]()
答:出射速度沿x轴正方向的质子,到达y轴所用的时间为 ![]() +
+ ![]() ;
;
(2)解:质子转过120°角后离开磁场,再沿直线到达图中P点,最后垂直电场方向进入电场,做类平抛运动,并到达y轴,运动轨迹如图中所示.
由几何关系可得P点距y轴的距离为:
x1=a+asin30°=1.5a
设在电场中运动的时间为 t3,由匀变速直线运动规律有:
x1= ![]()
即 t3= ![]()
质子在y轴方向做匀速直线运动,到达y轴时有:
y1=vt3=Ba ![]()
所以质子在y轴上的位置为:y=a+y1=a+Ba ![]()
答:出射速度与x轴正方向成30°角(如图中所示)的质子,到达y轴时的位置为a+2Ba ![]() ;
;
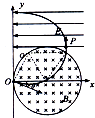
(3)解:若质子在y轴上运动最远,应是质子在磁场中沿右边界向上直行,垂直进入电场中做类平抛运动,
此时x′=2a
质子在电场中在y方向运动的距离为:y2=2Ba ![]()
质子离坐标原点的距离为:ym=a+y2=a+2Ba ![]()
由几何关系可证得,此题中凡进入磁场中的粒子,从磁场穿出时速度方向均与y轴平行,且只有进入电场中的粒子才能打到y轴上,因此
质子到达y轴的位置坐标的范围应是(a,a+2Ba ![]() )
)
答:质子到达y轴的位置坐标的范围为 (a,a+2Ba ![]() ).
).
【解析】(1)质子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力求解速度,质子进入电场后做类平抛运动,沿电场方向运动a后到达y轴,由匀变速直线运动规律求解;(2)质子转过120°角后离开磁场,再沿直线到达图中P点,最后垂直电场方向进入电场,做类平抛运动,并到达y轴,画出运动轨迹,根据几何关系结合运动学基本公式求解;(3)若质子在y轴上运动最远,应是质子在磁场中沿右边界向上直行,垂直进入电场中做类平抛运动,根据运动学基本公式求解质子离坐标原点的距离,再结合几何关系分析即可.