题目内容
【题目】如图所示，真空中两细束平行单色光a和b从一透明半球的左侧以相同速率沿半球的平面方向向右移动，光始终与透明半球的平面垂直。当b光移动到某一位置时，两束光都恰好从透明半球的左侧球面射出（不考虑光在透明介质中的多次反射后再射出球面）。此时a和b都停止移动，在与透明半球的平面平行的足够大的光屏M上形成两个小光点．已知透明半球的半径为R，对单色光a的折射率为n1=
，光束a和光束b之间的距离为
，光屏M到透明半球的平面的距离为L=（
＋
）R，不考虑光的干涉和衍射，真空中光速为c，求：
（1）单色光b在该透明半球的折射率。
（2）两束光从透明半球的平面入射直至到达光屏传播的时间差△t。
【答案】(1)2 (2)
【解析】解：（1）由
得，透明介质对a光的临界角为60O
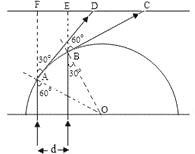
画出光路如图，A、B为两单色光在透明半球面的出射点，折射光线在光屏上形成光点D和C，AD、BC沿切线方向。设b光的临界角为θ，则由几何关系
，得
，故b光折射率为2
（2）a光在透明介质中
传播时间
在真空中：AD=R，∴
则
b光在透明介质中
传播时间
在真空中： 
则： 
∴
练习册系列答案
习题精选系列答案
相关题目
