��Ŀ����
1��С��ͬѧ�������ij���ɺϽ�����ƳɵĽ���˿�ĵ�����p���������˿�ĺ����ΪԲ�Σ�ʵ�������У����̶ȳߡ�������������ѹ��������Լ��ǧŷ����������������Լ��ŷ�������߱���������Դ��������������˿���������ɣ�
��1���ú��̶ȳ߲����䳤�ȣ�����������������ֱ��������ֱ���ͼ1��ͼ2��ʾ����ͼ��֪�䳤��L=59.40cm��ֱ��ΪD=0.434mm��
��2����ͬѧ�ƻ�Ҫ��ͼ������������ֵ��Ҫ���ѹ��0��ʼ�仯���뽫ͼ3��ʾʵ���·ͼ����ȱ���ֲ�ȫ��
��3��ͼ4��ʵ���в�õ�6�����I����ѹI����ѹU��ֵ��ĵ㣬��ͼ����ĵ���ֵR=5.95��������3λ��Ч���֣���
��4��д���������˿�ĵ�����p�ı���ʽ$\frac{��R{D}^{2}}{4L}$���ò�õ��������ķ��ű�ʾ����
���� ��1����ͼ����ʾ�̶���ȷ���̶ȳߵķֶ�ֵ����ͼ��֪������˿��һ���˵���̶ȳߵ���̶��߶��룬�����˿��һ�˵�����Ӧ�Ŀ̶ȳߵ�ʾ�����ǽ���˿�ij��ȣ�
�ȶ����������Ĺ̶��̶ȣ�Ȼ���ٶ��ɶ��̶ȣ��̶��̶ȼ��Ͽɶ��̶���0.01�ij˻��������������Ķ�����
��2�����ݵ�·ͼ���������·�ṹ��Ȼ����ݸ���·Ԫ�������ӷ�ʽ����ʵ���·ͼ��
��3����������ϵ������ĵ㣬��һ��ֱ�߰Ѿ����ܶ�ĵ���������������ͬһֱ���ϵĵ�Ҫ�ԳƵطֲ���ֱ�����࣬��ֱ�߾���U-Iͼ������U-Iͼ����ŷķ�������������ֵ��
��4����ŷķ�������������ֵ��Ȼ���ɵ��趨����������ʵı���ʽ��
��� �⣺��1����ͼ��֪���̶ȳߵķֶ�ֵ��1mm������˿�ij�����59.40cm����ͼ�ҿ�֪�����������Ĺ̶��̶�ʾ����0mm���ɶ��̶�ʾ����43.4�������������Ķ�����0mm+43.4��0.01mm=0.434mm��
��2������������С���������������ӷ���
����Ҫ���ѹ��0��ʼ�仯������������ѹʽ�ӷ���
��ͼ1��ʾ�� ͼ1��
ͼ1��
��3����㷨��ͼ��U-Iͼ����ͼ2��ʾ�� ͼ2��
ͼ2��
��U-Iͼ��ɵã�����˿���裺R=$\frac{2.5}{0.42}$=5.95����
��4������˿�ĺ���棺S=��r2=�У�$\frac{D}{2}$��2��
��R=�� $\frac{L}{S}$��
���Խ���˿�ĵ����ʣ���=$\frac{RS}{L}$=$\frac{��R{D}^{2}}{4L}$��
�ʴ�Ϊ����1��59.40��0.434����2����ͼ1��ʾ����3��5.95����4��$\frac{��R{D}^{2}}{4L}$��
���� ���⿼���˿̶ȳ������������Ķ�������·���Ϸ�������ʵ���·ͼ����U-Iͼ������衢������ʵı���ʽ�����⣬��ʵ��ij������⣬һ��Ҫ���գ������漰��֪ʶ��϶࣬���ѶȲ��Ǻܴ��������ջ���֪ʶ������ȷ���⣮

| A�� | ��Щ�����˶��Ľ��ٶ���ͬ | B�� | ��Щ�����˶������ٶ���ͬ | ||
| C�� | ��Щ�����˶����ļ��ٶ���ͬ | D�� | ��Щ�����˶������ٶȴ�С��� |
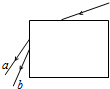 ��ͼ��ʾ��һ����ɫ��ӳ����岣��ש�ϱ������벣������������ש��Ӳ�����������Ϊa��b������ɫ�⣬��������ɫ����Ƚ�����˵����ȷ���ǣ�������
��ͼ��ʾ��һ����ɫ��ӳ����岣��ש�ϱ������벣������������ש��Ӳ�����������Ϊa��b������ɫ�⣬��������ɫ����Ƚ�����˵����ȷ���ǣ�������| A�� | �ڲ�����b���ȫ�����ٽ�ǽ�С | B�� | ������a��������ʽϴ� | ||
| C�� | �������a�Ⲩ���϶� | D�� | �ڲ�����b����ٶȽϴ� |
| X��m�� | 0.200 | 0.400 | 0.600 | 0.700 | 0.900 | 0.900 |
| t��s�� | 0.088 | 0.189 | 0.311 | 0.385 | 0.473 | 0.600 |
| $\frac{X}{t}$��m/s�� | 2.27 | 2.12 | 1.93 | 1.82 | 1.69 | 1.50 |

��1�����ݱ������������ݣ���ͼ2������ֽ�ϻ���$\frac{X}{t}$-tͼ�ߣ�
��2��������������$\frac{X}{t}$-tͼ�ߣ��ó�������ٶȵĴ�СΪa=3.0m/s2��
��3��������ˮƽ��ľ��֮��Ķ�Ħ������=0.31��
| A�� | ������������������µ��˶� | |
| B�� | ����ֻ�����������ɾ�ֹ��ʼ���˶� | |
| C�� | �������������ٶ������ij���Ϊ0���ȼ����˶� | |
| D�� | ����ǰn s��λ��֮��Ϊs1��s2��s3������sn=12��22��32������n2���˶� |
| A�� | T=2��$\sqrt{\frac{R^3}{GM}}$ | B�� | T=2��$\sqrt{\frac{{2{R^3}}}{GM}}$ | C�� | T=2��$\sqrt{\frac{{3{R^3}}}{GM}}$ | D�� | T=��$\sqrt{\frac{R^3}{GM}}$ |
 ��ͼ��ʾ�����ΪL�������㹻���Ĺ⻬ƽ�н�������̶���ˮƽ���ϣ����������ֲ�����ɣ�PG�Ҳಿ�ֵ�λ���ȵ���Ϊr0����PQ=QH=GH=L��PG��ർ����費�ƣ������AC�ĵ���ΪR0���������촦����ǿ�ų��У��ų�����ֱ�ڵ���ƽ�����£��Ÿ�Ӧǿ�ȴ�СΪB������Ϊm�ĵ����AC�ں���F�����´Ӿ�ֹ��ʼ�˶����ڵ���PG֮ǰ�����AC�Ѿ����٣�
��ͼ��ʾ�����ΪL�������㹻���Ĺ⻬ƽ�н�������̶���ˮƽ���ϣ����������ֲ�����ɣ�PG�Ҳಿ�ֵ�λ���ȵ���Ϊr0����PQ=QH=GH=L��PG��ർ����費�ƣ������AC�ĵ���ΪR0���������촦����ǿ�ų��У��ų�����ֱ�ڵ���ƽ�����£��Ÿ�Ӧǿ�ȴ�СΪB������Ϊm�ĵ����AC�ں���F�����´Ӿ�ֹ��ʼ�˶����ڵ���PG֮ǰ�����AC�Ѿ����٣� ��ͼ��һ��ľ��λ�ڹ⻬ˮƽ���ϣ���ľ�����˹̶�һ���壬ľ��͵����������ΪM=3.0kg��ľ��ij���ΪL=1.5m����ľ���Ҷ���һС��飬������m=1.0kg��С�����ľ���Ķ�Ħ��������=0.10�����Ƕ����ھ�ֹ״̬������С����Գ��ٶ�v0��ľ���������������ٶ�gȡ10m/s2��
��ͼ��һ��ľ��λ�ڹ⻬ˮƽ���ϣ���ľ�����˹̶�һ���壬ľ��͵����������ΪM=3.0kg��ľ��ij���ΪL=1.5m����ľ���Ҷ���һС��飬������m=1.0kg��С�����ľ���Ķ�Ħ��������=0.10�����Ƕ����ھ�ֹ״̬������С����Գ��ٶ�v0��ľ���������������ٶ�gȡ10m/s2��