题目内容
16.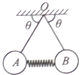 如图所示,两个完全相同的小球A、B用两根等长的轻绳悬挂在O点,两球质量均为m,两球之间夹着一根劲度系数为k的轻弹簧,两球静止不动时,弹簧处于水平方向,此时两根轻绳与水平方向之间的夹角均为θ,该弹簧的长度被压缩了( )
如图所示,两个完全相同的小球A、B用两根等长的轻绳悬挂在O点,两球质量均为m,两球之间夹着一根劲度系数为k的轻弹簧,两球静止不动时,弹簧处于水平方向,此时两根轻绳与水平方向之间的夹角均为θ,该弹簧的长度被压缩了( )| A. | $\frac{2mgtanθ}{k}$ | B. | $\frac{mgtanθ}{k}$ | C. | $\frac{mg}{ktanθ}$ | D. | $\frac{2mg}{ktanθ}$ |
分析 对A球受力分析,然后根据平衡条件并运用合成法得到弹簧的弹力,最后根据胡克定律得到弹簧的压缩量.
解答 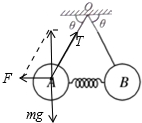 解:对球A受力分析,受重力mg、拉力T、弹簧的弹力F,如图
解:对球A受力分析,受重力mg、拉力T、弹簧的弹力F,如图
根据平衡条件,结合合成法,有:
Ftanθ=mg
根据胡克定律,有:
F=kx
联立解得:x=$\frac{mg}{ktanθ}$
故选:C
点评 本题关键是对小球受力分析,然后根据共点力平衡条件并运用合成法求解出弹力,最后根据胡克定律求解出弹簧的压缩量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.有一条两岸平行、河水均匀流动、流速恒为v的大河,小明驾着小船渡河,去程时船头朝向始终与河岸垂直,回程时行驶路线与河岸垂直.去程与回程所走的位移的比值为k,船在静水中的速度大小相同,则小船去程与回程所用时间的比值为( )
| A. | $\frac{k}{\sqrt{{k}^{2}-1}}$ | B. | $\frac{1}{\sqrt{{k}^{2}-1}}$ | C. | $\frac{1}{\sqrt{{k}^{2}-2}}$ | D. | $\sqrt{2-{k}^{2}}$ |
7.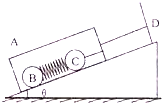 如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
 如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )
如图所示内壁光滑,质量为m的箱子A放在倾角为θ的光滑斜面上,为了防止箱子下滑用轻绳固定在斜面上的D柱,箱子中有质量均为m的小球B和C通过轻弹簧相连,然后C通过细绳固定在箱子上,求烧断箱子和D柱之间细线的瞬间,A、B的加速度分别为( )| A. | 0 0 | B. | 3gsinθ 0 | ||
| C. | $\frac{3}{2}$gsinθ 0 | D. | gsinθ gsinθ |
4.甲、乙两个物体沿同一直线向同一方向运动时,取物体的初速度方向为正方向,甲的初速度为2m/s,加速度恒为2m/s2.乙的初速度为10m/s,加速度恒为-3m/s2,则下列说法中正确的是( )
| A. | 两物体都做匀加速直线运动 | |
| B. | 甲做匀加速直线运动,它的速度变化较快 | |
| C. | 乙的速度变化率较大 | |
| D. | 乙的速度一直比甲大 |
11.随着太空技术的飞速发展,地球上人们登陆其它星球成为可能.假设未来的某一天,宇航员登上某一星球后,测得该星球表面的重力加速度是地球表面重力加速度的k倍,而该星球的平均密度与地球的差不多,则该星球质量大约是地球质量的( )
| A. | $\frac{1}{k}$倍 | B. | k倍 | C. | k2倍 | D. | k3倍 |
8.下列叙述中,符合物理学史实的是( )
| A. | 牛顿应用“理想斜面实验”推翻了亚里士多德“力是维持物体运动的原因”的观点 | |
| B. | 伽利略应用“斜面实验”研究了自由落体运动的规律 | |
| C. | 牛顿曾说“我之所以比别人看得远,是因为我站在了巨人的肩膀上”,牛顿所指的巨人是伽利略、笛卡尔等人 | |
| D. | 卡文迪许首先通过实验测出万有引力常量 |
5.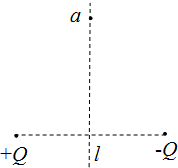 相距为l,带电量均为Q的正负点电荷的中垂线上,距离两个点电荷均为l的a点的电场强度的大小和方向( )
相距为l,带电量均为Q的正负点电荷的中垂线上,距离两个点电荷均为l的a点的电场强度的大小和方向( )
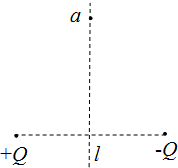 相距为l,带电量均为Q的正负点电荷的中垂线上,距离两个点电荷均为l的a点的电场强度的大小和方向( )
相距为l,带电量均为Q的正负点电荷的中垂线上,距离两个点电荷均为l的a点的电场强度的大小和方向( )| A. | Ea=k$\frac{Q}{{l}^{2}}$方向水平向左 | B. | Ea=$\sqrt{3}$k$\frac{Q}{{l}^{2}}$方向水平向左 | ||
| C. | Ea=k$\frac{Q}{{l}^{2}}$方向水平向右 | D. | Ea=$\sqrt{3}$k$\frac{Q}{{l}^{2}}$方向水平竖直向上 |
 如图所示,PQ、MN为足够长的两平行金属导轨,它们之间连接一阻值R=10Ω的电阻,两导轨间距L=1m,导轨平面与水平的夹角θ=30°,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上;一质量m=0.1kg的均匀金属杆ab放置在导轨上,杆ab与导轨PQ、MN垂直,杆ab与导轨间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,现让杆ab由静止开始沿导轨下滑,从杆ab开始下滑到恰好匀速运动的过程中,通过电阻R的电荷量q=0.6C,取重力加速度g=10m/s2,导轨和杆ab的电阻均不计.求杆ab:
如图所示,PQ、MN为足够长的两平行金属导轨,它们之间连接一阻值R=10Ω的电阻,两导轨间距L=1m,导轨平面与水平的夹角θ=30°,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上;一质量m=0.1kg的均匀金属杆ab放置在导轨上,杆ab与导轨PQ、MN垂直,杆ab与导轨间的动摩擦因数μ=$\frac{\sqrt{3}}{4}$,现让杆ab由静止开始沿导轨下滑,从杆ab开始下滑到恰好匀速运动的过程中,通过电阻R的电荷量q=0.6C,取重力加速度g=10m/s2,导轨和杆ab的电阻均不计.求杆ab: