题目内容
【题目】地铁列车从A站出发沿直线运动，行驶过程先做加速度大小为1m/s2的运动，经过一段时间后改做加速度大小为0.5m/s2的匀减速运动，到达B站时恰好零．若列车从A站到B站所用的总时间为90s．
（1）求AB两站间的距离．
（2）画出地铁列车从A站到B站的v一t图象．
【答案】
（1）
解：设加速运动时间为t，减速运动时间为t′
则加速获得的最大速度为v=a1t，
通过的位移 
减速运动，逆向看为初速度为零的匀加速直线运动，故v=a2t′
通过的位移 
所需总时间t总=t+t′
解得t=30s，t′=60s，v=30m/s
x1=450m，x2=900m
通过的总位移为：x=x1+x2=1350m
答： AB两站间的距离为1350m．
（2）
地铁列车从A站到B站的v一t图象如图所示
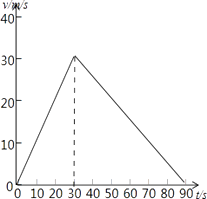
【解析】加速运动的末速度是减速运动的初速度，根据速度和时间关系求出加速运动和减速运动的时间比，根据匀变速直线运动的速度时间公式和位移时间公式即可求得．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
