题目内容
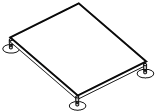
【题目】轻质弹簧原长为21，将弹資竖直放置在地面上，将一质最为m的物块置于弹簧顶端，缓慢下压物块直到弹簧长度为1释放，物块能上升的最大高度h=7.2m.水平光滑地面上固定着长也为21的平台A，平台上表面光滑。质量为m的小车Q左端靠着平台，质量为5m的木板B静置在地面上，小车和木板B的上表面都与平台等高，如图所示。现将上述弹簧水平放置，一端固定在平台A的左端，另一端与质量为m的物块P (可视为质点)接触但不连接，用外力推动物块P，将弹簧压缩至长度为1，由静止释放，P沿平台运动并滑上小车，当小车右端与木板B刚接触时，物块P恰好滑到小车右端且相对小车静止。已知小车Q长S=4.5m，木板B足够长。物块P与木板B之间的动摩擦因数μ=0.5，重力加速度g=10m/s，求：
(1)小车右端与木板B刚接触时的速度；
(2)平台A右端与木板B左端间的距离；
(3)小车与木板B、平台A碰撞时间极短且均无机械能损失，则小车从第一次与木板B相撞到第二次相撞经历的时间。(结果保留两位有效数字)
【答案】（1）6m/s （2）6.75m （3）3.2s
【解析】解：(1)设弹簧压缩l时，弹簧的弹性势能为EP，
由机械能守恒定律可得：EP=7.2mg
设物块P离开A平台的速度为
，由机械能守恒得： 
，解得：
以小车和物块P为一个系统，由动量守恒定律可得： 
解得： 
；
(2)以物块P离开平台到物块与小车共速过程中，物块位移为
，小车位移为
对物块P，由动能定理得： 
对小车，由动能定理得： 
位移关系： 
解得：平台右端与平台B左端的距离
；
(3)小车和木板B碰撞，由动量守恒定律和机械能守恒定律可知： 
联立解得： 
， 
物块P滑上木板B，设在第二次碰撞之间能与木板达到共速，由动时守恒定律：
，解得： 
所用时间： 
，解得： 
时间内木板B前进的位移
设小车与木板B第一次碰撞后回到第一次撞的位置的时间为
设总时间为t， 
解得 
。
