题目内容
【题目】如图所示，真空中有两块足够大的荧光屏P1、P2水平正对放置，间距为d，两荧光屏之间有一垂直于纸面向里的匀强磁场，磁感应强度大小为B．在紧贴荧光屏P2的A点有一粒子源，某一时刻向荧光屏P2上方纸面内的各个方向同时以相同的速率各发射一个粒子（图中只画出其中的几个方向），粒子的质量为m，带电荷量为-q，粒子的速率为v0=
．若粒子打到荧光屏上立即被吸收并发出荧光，不计粒子间的相互作用力和重力。
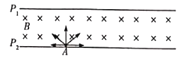
（1）求平行于P2向左发射的粒子在磁场中的运动时间；
（2）求荧光屏P1、P2之间有粒子经过的区域的面积；
（3）当平行于P2向左发射的粒子到达荧光屏时，求仍在磁场中运动的粒了和已经被屏吸收的粒子的个数之比。
【答案】（1）
；（2）
；（3）
。
【解析】
（1）设粒子运动轨迹的半径为R，则有：qv0B=
，解得：R=2d
平行于P2向左发射的粒子在磁场中的运动轨迹如图1所示，圆心角为α，
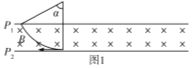
则有：cosα=
解得：α=
粒子的运动周期为：T=
粒子的运动时间为：t=
（2）粒子的轨迹恰好和Р1相切时，初速度的方向和P2成角θ轨迹如图2．所示，
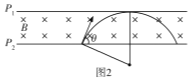
则有：cosθ=
即为：θ=
所以有粒子经过的区域的最大面积为：S=2（
πR2-
×Rcosα）+d×Rsinθ
解得：S=
（3）粒子的初速度方向与P2成角β时，轨迹如图3所示，
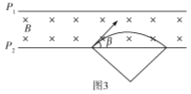
若圆心角也为，则β=
所以当平行于P2，向左发射的粒子到达P1时，此时已经打到荧光屏P1上的粒子的发射方向与平行于P2向右发射的粒子的方向成角的范围是θ～π已经打到荧光屏Р2上的粒子的发射方向与平行于P2向右的方向成角的范围是0～β仍在磁场中运动的粒子的发射方向范围是β-θ
所以仍在磁场中运动的粒子和和经被屏吸收的粒子个数之比为
=
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
