题目内容
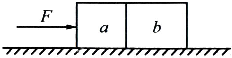
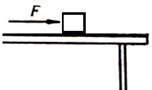
质量为M的斜面体置于水平面上,其上有质量的为m的物体,各面之间均为光滑.第一次将水平力F1加在m上,第二次将水平力F2加在M上,如图所示.两次都要求m,M间不发生滑动.求
.

| F1 |
| F2 |

左图中先对m受力分析,如图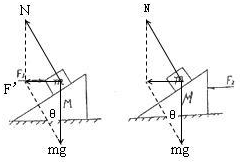
设斜面倾角为θ,由几何关系得到
F′=mgtanθ ①
由牛顿第二定律,得到
F1-F′=ma′②
再对整体运用牛顿第二定律
F1=(M+m)a′③
由①②③解得
F1=
右图中,先对m受力分析,受重力和支持力,结合运动情况,求出合力,如图
设斜面倾角为θ,由几何关系,得到
F合=mgtanθ
根据牛顿第二定律
a=
=gtanθ
再对整体研究,得到
F2=(M+m)a=(M+m)gtanθ
因而F1:F2=m:M
答:两次都要求m,M间不发生滑动,
为
.

设斜面倾角为θ,由几何关系得到
F′=mgtanθ ①
由牛顿第二定律,得到
F1-F′=ma′②
再对整体运用牛顿第二定律
F1=(M+m)a′③
由①②③解得
F1=
| (M+m)mgtanθ |
| M |
右图中,先对m受力分析,受重力和支持力,结合运动情况,求出合力,如图
设斜面倾角为θ,由几何关系,得到
F合=mgtanθ
根据牛顿第二定律
a=
| F合 |
| m |
再对整体研究,得到
F2=(M+m)a=(M+m)gtanθ
因而F1:F2=m:M
答:两次都要求m,M间不发生滑动,
| F1 |
| F2 |
| m |
| M |

练习册系列答案
相关题目