题目内容
如图所示．固定在水平桌面上的金属框架cdef，处在竖直向下匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动，此时abeb构成一个边长为L的正方形，棒的电阻为r，其余部分电阻不计，开始时磁感应强度为B0．
（1）若从t=0时刻起，磁感应强度B均匀增加，每秒增量为k，同时保持棒静止，求棒中的感应电流，在图上标出感应电流的方向；
（2）在上述（1）情况中，棒始终保持静止，当t=t1秒时需加的垂直于水平拉力为多大？
（3）若从t=0时刻起，磁感应强度B逐渐减小，当棒以恒定速度v向右做匀速运动时，可使棒中不产生感应电流．则磁感应强度B应怎样随时间t变化？（写出B与t的关系式）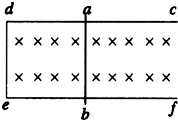
（1）若从t=0时刻起，磁感应强度B均匀增加，每秒增量为k，同时保持棒静止，求棒中的感应电流，在图上标出感应电流的方向；
（2）在上述（1）情况中，棒始终保持静止，当t=t1秒时需加的垂直于水平拉力为多大？
（3）若从t=0时刻起，磁感应强度B逐渐减小，当棒以恒定速度v向右做匀速运动时，可使棒中不产生感应电流．则磁感应强度B应怎样随时间t变化？（写出B与t的关系式）
（1）由题得：磁感应强度B的变化率
=kT/s，
由法拉第电磁感应定律知：
回路中感应电动势 E=
=
=kl2
感应电流 I=
根据楞次定律知感应电流方向为逆时针，即由b→a→d→e．
（2）当t=t1时，B=B0+kt1
安培力大小为F安=BIL
棒的水平拉力 F=F安=
（3）为了使棒中不产生感应电流，则回路中总磁通量不变．
t=0时刻，回路中磁通量为B0L2
设t时刻磁感应强度为B，此时回路中磁通量为BL（L+vt））
应有 BL（L+vt）=B0L2
则B=
磁感应强度随时间的变化规律是B=
答：
（1）棒中的感应电流大小为
，感应电流的方向为逆时针；
（2）棒始终保持静止，t=t1秒时需加的垂直于水平拉力为
．
（3）磁感应强度B的表达式为B=
．
| △B |
| △t |
由法拉第电磁感应定律知：
回路中感应电动势 E=
| △Φ |
| △t |
| △Bs |
| △t |
感应电流 I=
| kL2 |
| r |
根据楞次定律知感应电流方向为逆时针，即由b→a→d→e．
（2）当t=t1时，B=B0+kt1
安培力大小为F安=BIL
棒的水平拉力 F=F安=
| (B0+kt1)kL3 |
| r |
（3）为了使棒中不产生感应电流，则回路中总磁通量不变．
t=0时刻，回路中磁通量为B0L2
设t时刻磁感应强度为B，此时回路中磁通量为BL（L+vt））
应有 BL（L+vt）=B0L2
则B=
| B0L |
| L+vt |
磁感应强度随时间的变化规律是B=
| B0L |
| L+vt |
答：
（1）棒中的感应电流大小为
| kL2 |
| r |
（2）棒始终保持静止，t=t1秒时需加的垂直于水平拉力为
| (B0+kt1)kL3 |
| r |
（3）磁感应强度B的表达式为B=
| B0L |
| L+vt |
练习册系列答案
阅读快车系列答案
相关题目
如图所示，固定在水平面上的斜面倾角为θ，长方体木块A质量为M，其PQ面上钉着一枚小钉子，质量为m的小球B通过一细线与小钉子相连接，小球B与PQ面接触，且细线与PQ面平行，木块与斜面间的动摩擦因数为μ．下列说法正确的是（ ）
如图所示，固定在水平地面的倾角为θ斜面上，有一个竖直的挡板，质量为m的光滑圆柱处于静止状态．求：
如图所示，固定在水平桌面上的有缺口的方形木块，abcd为半径为R（已知量）的四分之三圆周的光滑轨道，a为轨道的最高点，de面水平且有足够长度．今将质量为m的小球在d点的正上方某一高度为h（未知量）处由静止释放，让其自由下落到d处切入轨道内运动，小球恰能通过a点，（不计空气阻力，已知重力加速度为g）求：
如图所示斜面固定在水平地面上，斜面倾角θ=37°，斜面足够长，物体与斜面间的动摩擦因数μ=0.5．一质量为1kg的物体以v0=4m/s的初速度从斜面底端向上．sin37°=0.6，cos37°=0.8，g取10m/s2，求
如图所示，固定在水平面上的斜面倾角为θ，长方体木块A的质量为M，其PQ面上钉着一枚小钉子，质量为m的光滑小球B通过一细线与小钉子相连接，细线与斜面垂直，以下说法正确的是 （不计空气阻力，重力加速度为g）（ ）| A、若木块匀速下滑，则小球对木块的压力为零 | B、若木块与斜面的动摩擦因数为μ且木块匀速下滑，则小球对木块的压力大小为μmgcosθ | C、若木块与斜面的动摩擦因数为μ且木块匀加速下滑，则小球对木块的压力大小为mgsinθ | D、若斜面光滑，则小球对木块的压力为零 |