题目内容
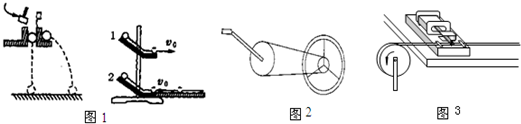
 如图所示斜面固定在水平地面上,斜面倾角θ=37°,斜面足够长,物体与斜面间的动摩擦因数μ=0.5.一质量为1kg的物体以v0=4m/s的初速度从斜面底端向上.sin37°=0.6,cos37°=0.8,g取10m/s2,求
如图所示斜面固定在水平地面上,斜面倾角θ=37°,斜面足够长,物体与斜面间的动摩擦因数μ=0.5.一质量为1kg的物体以v0=4m/s的初速度从斜面底端向上.sin37°=0.6,cos37°=0.8,g取10m/s2,求(1)物体上滑的最大距离?
(2)物体从斜面顶端返回斜面底端的时间?
分析:(1)由牛顿第二定律可以求出物体上滑时的加速度,当物体的速度减至零时到达斜面的最高点,根据运动学公式求出最大位移的大小;
(2)由牛顿第二定律求得加速度,根据位移公式求解时间.
(2)由牛顿第二定律求得加速度,根据位移公式求解时间.
解答:解:(1)物体上滑时,由牛顿第二定律得:mgsinθ+μmgcosθ=ma
解得:a=10m/s2.
由匀变速运动的速度位移公式可知,物体上滑的最大距离:
x=
=
=0.8m;
(2)物体下滑过程中,由牛顿第二定律得:
mgsinθ-μmgcosθ=ma′
解得:a′=2m/s2.
由x=
a′t2可知,物体下滑的时间:
t=
=
≈0.89s;
答:(1)物体沿斜面上滑的最大位移的大小为0.8m;
(2)物体从斜面顶端返回斜面底端的时间为0.89s.
解得:a=10m/s2.
由匀变速运动的速度位移公式可知,物体上滑的最大距离:
x=
| ||
| 2a |
| 42 |
| 2×10 |
(2)物体下滑过程中,由牛顿第二定律得:
mgsinθ-μmgcosθ=ma′
解得:a′=2m/s2.
由x=
| 1 |
| 2 |
t=
|
|
答:(1)物体沿斜面上滑的最大位移的大小为0.8m;
(2)物体从斜面顶端返回斜面底端的时间为0.89s.
点评:本题是两个过程的问题,运用动能定理、牛顿第二定律和运动学规律结合进行处理,还要抓住两个过程的位移大小相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
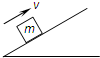
 如图所示,A、B两小球由绕过轻质定滑轮的细线相连,B球放在倾角为α的固定光滑斜面上,A球放在装有水的容器底部(容器底部直径足够大).现用手控制住B球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A球的质量为m,重力加速度为g,细线与滑轮之间的摩擦不计,图示状态水的深度为h,A球的体积为V,开始时整个系统处于静止状态.释放B球后,B球沿斜面下滑至速度最大时A球恰好离开水面一半,不计大气压强.下列说法正确的是( )
如图所示,A、B两小球由绕过轻质定滑轮的细线相连,B球放在倾角为α的固定光滑斜面上,A球放在装有水的容器底部(容器底部直径足够大).现用手控制住B球,并使细线刚刚拉直但无拉力作用,并保证滑轮左侧细线竖直、右侧细线与斜面平行.已知A球的质量为m,重力加速度为g,细线与滑轮之间的摩擦不计,图示状态水的深度为h,A球的体积为V,开始时整个系统处于静止状态.释放B球后,B球沿斜面下滑至速度最大时A球恰好离开水面一半,不计大气压强.下列说法正确的是( )| A、B球沿斜面下滑至速度最大的过程中,B球的机械能增加 | B、从释放B球到A球刚离开水面一半的过程中,A、B两小球组成的系统机械能守恒 | C、在A球再次落到容器底前,A、B两小球和水组成的系统机械能守恒 | D、根据上述条件可以求出B球的质量 |
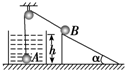
 某同学设计了如图所示的实验:将两个斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是球1落到光滑水平板上并击中球2,这说明球1( )
某同学设计了如图所示的实验:将两个斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是球1落到光滑水平板上并击中球2,这说明球1( )| A、水平方向的分运动是匀速直线运动 | B、水平方向的分运动是匀加速直线运动 | C、竖直方向的分运动是自由落体运动 | D、竖直方向的分运动是匀速直线运动 |
 如左图所示的演示实验中,A、B两球同时落地,说明
如左图所示的演示实验中,A、B两球同时落地,说明 某同学设计了如图所示的实验:将两个相同斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是
某同学设计了如图所示的实验:将两个相同斜滑道固定在同一竖直面内,最下端水平.把两个质量相等的小钢球从斜面的同一高度由静止同时释放,滑道2与光滑水平板吻接,则将观察到的现象是