题目内容
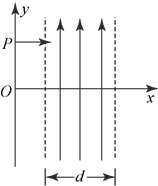
【题目】如图所示,坐标原点O处有一点状的放射源,它向xOy平面内的x轴上各个方向发射![]() 粒子,
粒子, ![]() 粒子的速度大小都是
粒子的速度大小都是![]() ,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为
,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为![]() ,其中q与m分别为
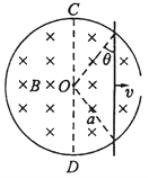
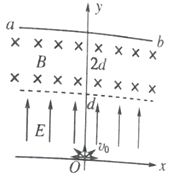
,其中q与m分别为![]() 粒子的电荷量和质量;在d<y<2d的区域内分布有垂直于xOy平面的匀强磁场. ab为一块很大的平面感光板,放置于y=2d处,如图所示. 观察发现此时恰无粒子打到ab板上. (不考虑
粒子的电荷量和质量;在d<y<2d的区域内分布有垂直于xOy平面的匀强磁场. ab为一块很大的平面感光板,放置于y=2d处,如图所示. 观察发现此时恰无粒子打到ab板上. (不考虑![]() 粒子的重力)
粒子的重力)
(1)求![]() 粒子刚进入磁场时的动能;
粒子刚进入磁场时的动能;
(2)求磁感应强度B的大小;
(3)将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被![]() 粒子打中的区域的长度.
粒子打中的区域的长度.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:根据动能定理求出α粒子刚进人磁场时的动能;粒子沿x轴正方向射出的粒子进入磁场偏转的角度最大,若该粒子进入磁场不能打在ab板上,则所有粒子均不能打在ab板上,根据带电粒子在电场中类平抛运动,求出进入磁场中的偏转角度,结合几何关系得出轨道半径,从而得出磁感应强度的大小;沿x轴负方向射出的粒子若能打到ab板上,则所有粒子均能打到板上.其临界情况就是此粒子轨迹恰好与ab板相切.根据带电粒子在磁场中运动的轨道半径大小得出磁场的宽度,从而确定出ab板移动的位置,根据几何关系求出ab板上被α粒子打中的区域的长度。
(1)根据动能定理: ![]()
α粒子刚进人磁场时的动能为: ![]()
(2)根据(1)中结果可知![]() ,
,
对于沿x轴正方向射出的粒子进入磁场时与x轴正方向夹角![]()
其在电场中沿x轴方向的位移: 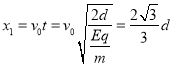
该粒子运动轨迹如图所示:
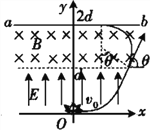
根据几何知识可知:若该粒子不能打到ab板上,则所有粒子均不能打到ab板上,因此该粒子轨迹必与ab板相切,其圆周运动的半径满足关系式为: ![]()
解得: ![]() ,又根据洛伦兹力提供向心力:
,又根据洛伦兹力提供向心力: ![]()
可得: ![]()
(3)根据几何知识可知,沿x轴负方向射出的粒子若能打到ab板上,则所有粒子均能打到ab板上,其临界情况就是此粒子轨迹恰好与ab板相切
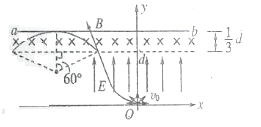
由图可知此时磁场宽度应为原来的![]()
即当此板位于![]() 的位置时,恰好所有粒子均
的位置时,恰好所有粒子均
能打到板上,且ab板上被打中区域的长度为: ![]()

 备战中考寒假系列答案
备战中考寒假系列答案