题目内容
10.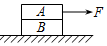 如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )
如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )| A. | 当拉力F<20N时,两物体保持相对静止状态 | |
| B. | 两物体始终没有相对运动 | |
| C. | 两物体从受力开始就有相对运动 | |
| D. | B物体的加速度不会超过3m/s2 |
分析 隔离对B分析,求出AB发生相对滑动时的临界加速度,再对整体分析,运用牛顿第二定律求出刚好发生相对滑动时的拉力.
解答 解:隔离对B分析,当AB间摩擦力达到最大静摩擦力时,A、B发生相对滑动,则:aB=$\frac{μ{m}_{A}g}{{m}_{B}}$=$\frac{0.2×6×10}{2}$=6m/s2,再对整体:F=(mA+mB)a=8×6N=48N.知当拉力达到48N时,A、B才发生相对滑动.所以:
A、当拉力F<20N时,两物体保持相对静止状态,故A正确;
BC、当F从10N逐渐增加,在F增大到25N的过程中,都未超过48N,所以两物体始终没有相对运动,故B正确,C错误;
D、由上述分析可知,A、B发生相对滑动,则:aB=6m/s2,故D错误.
故选:AB.
点评 本题主要考查牛顿第二定律的临界问题,关键找出临界状态,运用整体法和隔离法,根据牛顿第二定律进行求解.

练习册系列答案
相关题目
20.关于万有引力定律下述说法正确的是( )
| A. | 万有引力定律是英国物理学家卡文迪许首先发现的 | |
| B. | 引力常量G是比例系数,没有单位 | |
| C. | 牛顿得出万有引力定律同时测量出了引力常量G的值 | |
| D. | 第谷、开普勒、牛顿、卡文迪许是对发现和完善万有引力定律有贡献的科学家 |
18.矩形线圈绕垂直于匀强磁场的对称轴做匀速转动,当线圈通过中性面时,则以下说法错误的是( )
| A. | 线圈平面与磁场方向垂直 | |
| B. | 线圈中的感应电动势的方向将发生变化 | |
| C. | 通过线圈的磁通量达到最大值 | |
| D. | 通过线圈的磁通量的变化率达到最大值 |
5.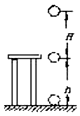 如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )
如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )
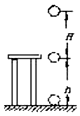 如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )
如图从离地面高为h的桌面上以速度v竖直向上抛出质量为m的物体,它上升H后又返回下落,最后落在地面上,则下列说法中正确的是(不计空气阻力,以地面为参考面)( )| A. | 物体在最高点时机械能为mg(H+h) | |
| B. | 物体落地时的机械能为mg(H+h)+$\frac{1}{2}$mv2 | |
| C. | 物体落地时的机械能为mgh+$\frac{1}{2}$mv2 | |
| D. | 物体在落回过程中,经过桌面时的机械能为mgH |
15.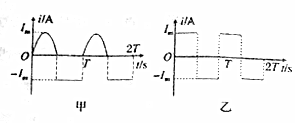 两只相同的电阻,分别通过两种如图甲、乙所示波形的交流电,则在一个周期内,两电阻产生的热量之比$\frac{{Q}_{甲}}{{Q}_{乙}}$等于( )
两只相同的电阻,分别通过两种如图甲、乙所示波形的交流电,则在一个周期内,两电阻产生的热量之比$\frac{{Q}_{甲}}{{Q}_{乙}}$等于( )
 两只相同的电阻,分别通过两种如图甲、乙所示波形的交流电,则在一个周期内,两电阻产生的热量之比$\frac{{Q}_{甲}}{{Q}_{乙}}$等于( )
两只相同的电阻,分别通过两种如图甲、乙所示波形的交流电,则在一个周期内,两电阻产生的热量之比$\frac{{Q}_{甲}}{{Q}_{乙}}$等于( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
2. 如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )
如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )
 如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )
如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )| A. | $\frac{1}{4}$g | B. | $\frac{1}{3}$g | C. | $\frac{2}{3}$g | D. | g |
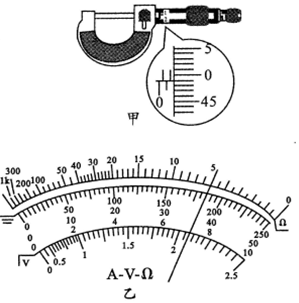 导电玻璃是制造LCD的主要材料之一.为测量导电玻璃的电阻率,某小组同学选取了一个长度为L的圆柱体导电玻璃器件,上面标有“3V,L”的字样,主要步骤如下,完成下列问题:
导电玻璃是制造LCD的主要材料之一.为测量导电玻璃的电阻率,某小组同学选取了一个长度为L的圆柱体导电玻璃器件,上面标有“3V,L”的字样,主要步骤如下,完成下列问题: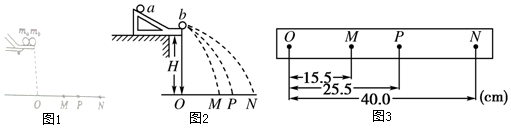
 光滑的水平面上,用弹簧相连的质量均为1kg的A、B两物块都以v0=6m/s的速度向右运动,弹簧处于原长,质量为2kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动,在以后的运动中,当弹簧的弹性势能达到最大为6J时,物块A的速度是3m/s.
光滑的水平面上,用弹簧相连的质量均为1kg的A、B两物块都以v0=6m/s的速度向右运动,弹簧处于原长,质量为2kg的物块C静止在前方,如图所示.B与C碰撞后二者粘在一起运动,在以后的运动中,当弹簧的弹性势能达到最大为6J时,物块A的速度是3m/s.