题目内容
2. 如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )
如图所示,天花板上固定有一光滑的定滑轮,绕过定滑轮且不可伸长的轻质细绳左端悬挂一质量为M的铁块;右端悬挂有两质量均为m的铁块,上下两铁块用轻质细线连接,中间夹一轻质弹簧处于压缩状态,此时细线上的张力为2mg,最初系统处于静止状态.某瞬间将细线烧断,则左端铁块的加速度大小为( )| A. | $\frac{1}{4}$g | B. | $\frac{1}{3}$g | C. | $\frac{2}{3}$g | D. | g |
分析 分析题意,根据绳子上拉力为2mg,对M分析可明确M与m间的关系,再对右上m分析,由平衡条件可知弹簧的弹力;烧断细线后弹簧的弹力不变,对M和右上m分析,由牛顿第二定律可求得M的加速度.
解答 解:由题意可知,烧断细线前轻绳了上的张力为2mg,根据平衡条件可知M=2m,以右上端的铁块为研究对象,根据平衡条件可知,烧断细线前弹簧的弹力为mg,方向向上;
细线烧断的瞬时,铁块M与右上的铁块m间的轻绳张力也会发生变化,但二者的加速度大小相同,沿绳子方向对两物体分析,根据牛顿第二定律可得:
2mg+mg-mg=3ma
解得:a=$\frac{2}{3}$g;
故C正确,ABD错误.
故选:C.
点评 本题考查牛顿第二定律应用中的动态分析问题,本题关键点在于明确弹簧是处于压缩状态的,所以分析时要以右上的m分析,不能分析右下的物体,同时注意应用牛顿第二定律时是沿绳子方向列牛顿第一定律方程.

练习册系列答案
相关题目
12.对地球同步卫星,下列说法正确的是( )
| A. | 只能定点在赤道的正上方,质量不同的同步卫星轨道半径都相同 | |
| B. | 运行的角速度与地球自转角速度相同,相对地球静止 | |
| C. | 轨道半径都相同,以第一宇宙速度运行 | |
| D. | 可在我国的北京上空运行 |
10.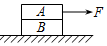 如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )
如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )
 如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )
如图所示,物体A叠放在物体B上,B置于光滑水平面上.A、B质量分别为mA=6kg,mB=2kg,A、B之间的动摩擦因数μ=0.2.开始时F=10N,此后F逐渐增加,则在F增大到25N的过程中,下列说法正确的是( )| A. | 当拉力F<20N时,两物体保持相对静止状态 | |
| B. | 两物体始终没有相对运动 | |
| C. | 两物体从受力开始就有相对运动 | |
| D. | B物体的加速度不会超过3m/s2 |
17.交流电压的表达式为u=100$\sqrt{2}$sin100πtV,可知( )
| A. | 用电压表测该电压其示数为50V | |
| B. | 该交流电压的周期为0.02s | |
| C. | 将该电压在“100V 100W”的灯泡两端,灯泡的实际功率小于100W | |
| D. | t=$\frac{1}{400}$s时,该交流电压的瞬时值为50V |
7.关于下列器材的原理和用途,叙述正确的是( )
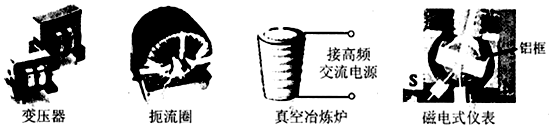

| A. | 变压器可以改变交流电压与稳恒直流电压 | |
| B. | 扼流圈对变化的电流有阻碍作用 | |
| C. | 真空冶炼炉的工作原理是通过线圈发热使炉内金属熔化 | |
| D. | 磁电式仪表用来做线圈骨架的铝框能起到电磁阻尼的作用 |
11.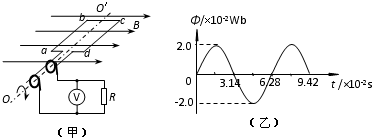 如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
 如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )
如图甲所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在匀强磁场中绕垂直于磁场方向的固定轴OO′匀速转动,线圈的匝数n=100、电阻r=10Ω,线圈的两端经集流环与电阻R连接,电阻R=90Ω,与R并联的交流电压表为理想电表,除线圈电阻r和外电阻R,其余电阻均不计,在t=0时刻,线圈平面与磁场方向平行,穿过每匝线圈的磁通量φ随时间t按图乙所示正弦规律变化,取π=3.14,下列说法正确的是( )| A. | 交流发电机产生的电动势的有效值为100$\sqrt{2}$V | |
| B. | 穿过线圈磁通量变化率的最大值为2×10-2V | |
| C. | 电路中交流电压表的示数为180V | |
| D. | 若规定t=0时的电流方向为正,则从此时开始发电机产生的电动势随时间变化的关系为e=200cos100t(V) |
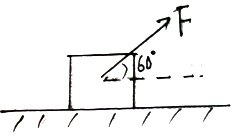 如图所示,静止在光滑水平面上的物体质量为25kg,在与水平方向成60°角斜向上的力F作用下运动10s.已知F=10N,求:
如图所示,静止在光滑水平面上的物体质量为25kg,在与水平方向成60°角斜向上的力F作用下运动10s.已知F=10N,求: