题目内容
【题目】如图所示，工人用绳索拉铸件，铸件的质量是20kg，铸件与地面间的动摩擦因数是0.25．工人用80N的力拉动铸件，从静止开始在水平面上前进，绳与水平方向的夹角为α=37°．并保持不变，经4s后松手．问松手后铸件还能前进多远？（g=l0m/s2）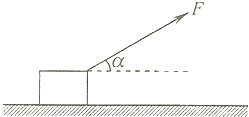
【答案】解：工人拉铸件时，根据牛顿运动定律有：
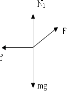
Fcosα﹣f=ma1
N1+fsinα﹣mg=0
f=μN1
由以上三式，代入数据得：a1=1.3 m/s2
松手时，工件的速度为：v=a1t=1.3×4=5.2m/s
设松手后，工件的加速度为a2，根据牛顿第二定律有：μmg=ma2
代入数据解得：a2=2.5 m/s2
松手后，工件滑行的距离是： 
= 
=5.4 m
答：松手后铸件还能前进5.4m．
【解析】根据牛顿第二定律求出在拉力作用下的加速度，根据速度时间公式求出松手后的速度，再根据牛顿第二定律求出撤去拉力后的加速度，结合速度位移公式求出松手后铸件还能滑行的距离．
【考点精析】通过灵活运用匀变速直线运动的速度、位移、时间的关系，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值即可以解答此题．
练习册系列答案
相关题目
