题目内容
【题目】如图所示,水平放置的平行金属导轨宽度为d=1m,导轨间接有一个阻值为R=2Ω的灯泡,一质量为m=1Kg的金属棒跨接在导轨之上,其电阻为r=1Ω,且和导轨始终接触良好,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直导轨平面向下,现对金属棒施加一水平向右的拉力F,使金属棒从静止开始向右运动.求: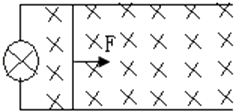
(1)若金属棒与导轨间的动摩擦因数为μ=0.2,施加的水平恒力为F=10N,则金属棒达到的稳定速度v1的大小;
(2)若金属棒与导轨间的动摩擦因数为μ=0.2,施加的水平力功率为P=6W,则金属棒达到的稳定速度v2的大小;
(3)若金属棒与导轨间是光滑的,施加的水平力功率恒为P=20W,经历t=1s的过程中灯泡产生的热量为QR=12J,则此时金属棒的速度v3的大小.
【答案】
(1)解:金属棒做匀速直线运动时达到稳定状态,
安培力:F安培=BId= ![]() ,
,
由平衡条件得:F=μmg+ ![]() ,
,
代入数据解得:v1=6m/s;
答:若金属棒与导轨间的动摩擦因数为μ=0.2,施加的水平恒力为F=10N,则金属棒达到的稳定速度v1的大小为6m/s;
(2)解:金属棒做匀速直线运动时达到稳定状态,
安培力:F安培=BId= ![]() ,拉力:F=
,拉力:F= ![]() ,
,
由平衡条件得: ![]() =μmg+
=μmg+ ![]() ,
,
代入数据解得:v2=1.5m/s;
答:若金属棒与导轨间的动摩擦因数为μ=0.2,施加的水平力功率为P=6W,则金属棒达到的稳定速度v2的大小为1.5m/s;
(3)解:由焦耳定律:Q=I2Rt可知:QR:Qr=R:r=2:1,则:Qr= ![]() QR=6J,
QR=6J,
由能量守恒定律得:Pt=QR+Qr+ ![]() mv32,
mv32,
代入数据解得:v3=2m/s;
答:若金属棒与导轨间是光滑的,施加的水平力功率恒为P=20W,经历t=1s的过程中灯泡产生的热量为QR=12J,则此时金属棒的速度v3的大小为2m/s.
【解析】(1)金属棒到达稳定时做匀速直线运动,由安培力公式求出安培力,然后由平衡条件求出金属棒的速度.(2)金属棒达到稳定时做匀速直线运动,应用安培力公式、平衡条件、功率公式求出稳定时的速度.(3)由能量守恒定律求出金属棒的速度.
【考点精析】本题主要考查了电磁感应与力学和能量守恒定律的相关知识点,需要掌握用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向;求回路中电流强度;分析研究导体受力情况(包含安培力,用左手定则确定其方向);列动力学方程或平衡方程求解;能量守恒定律:能量既不会消灭,也不会创生,它只会从一种形式转化为其他形式,或者从一个物体转移到另一个物体,而在转化和转移过程中,能量的总量保持不变才能正确解答此题.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案