题目内容
12.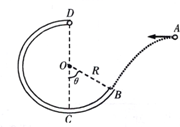 如图所示,BCD为一竖直放置,半径为R的光滑圆弧细管道,BC弧对应的圆心角θ=60°,连线DC是圆弧细管道的竖直直径,一质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆弧细管BCD的B点沿该处切线方向进入圆弧细管道,经BCD从圆弧细管道的最高点D射出,且经过D点时小球对内侧管道的压力大小为$\frac{3}{4}$mg,不计空气阻力,已知重力加速度大小为g,求:
如图所示,BCD为一竖直放置,半径为R的光滑圆弧细管道,BC弧对应的圆心角θ=60°,连线DC是圆弧细管道的竖直直径,一质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆弧细管BCD的B点沿该处切线方向进入圆弧细管道,经BCD从圆弧细管道的最高点D射出,且经过D点时小球对内侧管道的压力大小为$\frac{3}{4}$mg,不计空气阻力,已知重力加速度大小为g,求:(1)小球经过D点时的速度大小;
(2)小球从A点水平抛出的初速度大小.
分析 (1)由已知条件可知向心力,再由牛顿第二定律和向心力公式可求得速度;
(2)由机械能守恒定律和平抛运动规律列式,联立可求得初速度.
解答 解:(1)设小球经过D点时的速度大小为v1,由题意及牛顿第二定律可得:
mg-$\frac{3}{4}mg$=m$\frac{{v}_{1}^{2}}{R}$
解得:v1=$\frac{\sqrt{gR}}{2}$;
(2)设小球在B点时的速度大小为v,由机械能守恒定律可得:
$\frac{1}{2}$mv2=$\frac{1}{2}$mv12+mg(R+Rcosθ)
设小球从A点到水平抛出的初速度大小为v0;根据平抛运动规律可得:
cosθ=$\frac{{v}_{0}}{v}$
联立解得:v0=$\frac{\sqrt{13Rg}}{4}$
答:(1)小球经过D点时的速度大小为$\frac{\sqrt{gR}}{2}$
(2)小球从A点水平抛出的初速度大小$\frac{\sqrt{13Rg}}{4}$.
点评 本题考查向心力公式、平抛及机械能守恒定律的应用,要注意正确选择物理过程,明确物理规律的应用求解.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3. 如图所示,质量为1kg的小球从桌面竖直上抛,到达的最大高度为0.8m,返回后,落到桌面下1m的地面上,取桌面为零重力势能的参考平面,g=10m/s2,则下述说法正确的是( )
如图所示,质量为1kg的小球从桌面竖直上抛,到达的最大高度为0.8m,返回后,落到桌面下1m的地面上,取桌面为零重力势能的参考平面,g=10m/s2,则下述说法正确的是( )
 如图所示,质量为1kg的小球从桌面竖直上抛,到达的最大高度为0.8m,返回后,落到桌面下1m的地面上,取桌面为零重力势能的参考平面,g=10m/s2,则下述说法正确的是( )
如图所示,质量为1kg的小球从桌面竖直上抛,到达的最大高度为0.8m,返回后,落到桌面下1m的地面上,取桌面为零重力势能的参考平面,g=10m/s2,则下述说法正确的是( )| A. | 小球在最高点时机械能最大 | B. | 小球在桌面时重力势能最小 | ||
| C. | 小球落地前瞬间具有的机械能为8J | D. | 小球落地前瞬间具有的动能为8J |
20. 如图所示,质量相等的A、B两物体紧贴在半径不同的圆筒竖直内壁上,随圆微一起以MN为转轴做匀速圆周运动,设匀速转动过程中A、B两物体受到的摩擦力大小分别为fA、fB,所受弹力大小分别为FA、FB,则下列关系正确的是( )
如图所示,质量相等的A、B两物体紧贴在半径不同的圆筒竖直内壁上,随圆微一起以MN为转轴做匀速圆周运动,设匀速转动过程中A、B两物体受到的摩擦力大小分别为fA、fB,所受弹力大小分别为FA、FB,则下列关系正确的是( )
 如图所示,质量相等的A、B两物体紧贴在半径不同的圆筒竖直内壁上,随圆微一起以MN为转轴做匀速圆周运动,设匀速转动过程中A、B两物体受到的摩擦力大小分别为fA、fB,所受弹力大小分别为FA、FB,则下列关系正确的是( )
如图所示,质量相等的A、B两物体紧贴在半径不同的圆筒竖直内壁上,随圆微一起以MN为转轴做匀速圆周运动,设匀速转动过程中A、B两物体受到的摩擦力大小分别为fA、fB,所受弹力大小分别为FA、FB,则下列关系正确的是( )| A. | fA>fB | B. | fA<fB | C. | FA>FB | D. | FA<FB |
17.以下的计时数据中指时间间隔的是( )
| A. | 2010年4月14日7时49分,我国青海玉树发生7.1级地震 | |
| B. | 第十六届亚运会于2010年11月12日在广州开幕 | |
| C. | 刘翔创造了12.88秒的110米栏的较好成绩 | |
| D. | 我国航天员翟志刚在“神七”飞船外完成了历时20分钟的太空行走 |
1. 如图所示,两个质量均为m=5×10-7kg的小球,分別固定在长l=30cm的两细丝线的一端,两丝线的只一端固定于同-点O.当两小球带上等量正电荷,两球静止时两丝线间夹角为α=90°(两小球可看成点电荷).则每个小球的带电量( )
如图所示,两个质量均为m=5×10-7kg的小球,分別固定在长l=30cm的两细丝线的一端,两丝线的只一端固定于同-点O.当两小球带上等量正电荷,两球静止时两丝线间夹角为α=90°(两小球可看成点电荷).则每个小球的带电量( )
 如图所示,两个质量均为m=5×10-7kg的小球,分別固定在长l=30cm的两细丝线的一端,两丝线的只一端固定于同-点O.当两小球带上等量正电荷,两球静止时两丝线间夹角为α=90°(两小球可看成点电荷).则每个小球的带电量( )
如图所示,两个质量均为m=5×10-7kg的小球,分別固定在长l=30cm的两细丝线的一端,两丝线的只一端固定于同-点O.当两小球带上等量正电荷,两球静止时两丝线间夹角为α=90°(两小球可看成点电荷).则每个小球的带电量( )| A. | 1×10-6C | B. | 1×10-7C | C. | 1×10-8C | D. | 3×10-9C |

 如图所示,在平面坐标XOY内有垂直纸面向外的匀强磁场,A、B两点分别在Y轴上和X轴上,到原点O的距离分别为a和$\sqrt{3}$a,一正粒子以大小为V0的初速度从原点O出发恰好能经过A点和B点,已知正粒子的质量为m,电荷量为q,不计粒子的重力,求:
如图所示,在平面坐标XOY内有垂直纸面向外的匀强磁场,A、B两点分别在Y轴上和X轴上,到原点O的距离分别为a和$\sqrt{3}$a,一正粒子以大小为V0的初速度从原点O出发恰好能经过A点和B点,已知正粒子的质量为m,电荷量为q,不计粒子的重力,求: