题目内容
5. 质量为5kg的物块甲从倾角为37°的传输带上端静止下滑,传送带向上匀速转动,其速度v=1m/s,传送带AB长度为16米,物块进入水平地面CD后与放在水平地面CD上距C点x1=1m处的物块乙相碰,结果乙进入光滑半圆弧轨道DE,并恰好能到达半圆轨道的最高点E,传送带与水平地面之间光滑连接(光滑圆弧BC长度可忽略),水平面CD长度为1.8米,物块与水平地面及传送带的动摩擦因数均为μ=0.5,圆弧DE半径R=0.8m,物块乙的质量为1kg,g取10m/s2.试求:
质量为5kg的物块甲从倾角为37°的传输带上端静止下滑,传送带向上匀速转动,其速度v=1m/s,传送带AB长度为16米,物块进入水平地面CD后与放在水平地面CD上距C点x1=1m处的物块乙相碰,结果乙进入光滑半圆弧轨道DE,并恰好能到达半圆轨道的最高点E,传送带与水平地面之间光滑连接(光滑圆弧BC长度可忽略),水平面CD长度为1.8米,物块与水平地面及传送带的动摩擦因数均为μ=0.5,圆弧DE半径R=0.8m,物块乙的质量为1kg,g取10m/s2.试求:(1)物块甲在传送带上滑动产生的热量;
(2)碰撞后一瞬间物块乙的速度.
分析 (1)分析滑块下滑过程中相对位移,由摩擦力与相对位移的乘积可求得热量;
(2)分别对甲、乙两物体分析,由动能定理可求得甲球碰前及乙球碰后的速度.
解答 解:(1)传送带上运动,则摩擦力一直向上,则物块的加速度为:
a=$\frac{mgsin37°-μmgcos37°}{m}$=gsin37°-μgcos37°=10×0.6-0.5×10×0.8=2m/s2.
物体下滑到底部的时间为:t=$\sqrt{\frac{2{x}_{AB}}{a}}$=$\sqrt{\frac{2×16}{2}}$=4s;
此时传送带的位移为:s传送带=vt=1×4=4m,
相对位移为:x=s传送带+16=4+16=20m,
则产生的热量为:Q=μmgcos37°x=0.5×5×10×0.8×20=400J;
(2)物块甲到达C点的速度为:vC=at=2×4=8m/s,
物体由C到乙的位置时,由动能定理可得:
-μmgx1=$\frac{1}{2}$mv甲2-$\frac{1}{2}$mvC2,解得:v甲=$\sqrt{54}$m/s;
碰后乙恰好到达最高点,由牛顿第二定律得:m乙g=m乙$\frac{{v}^{2}}{R}$,
解得:v=$\sqrt{gR}$=$\sqrt{10×0.8}$=$\sqrt{8}$m/s,
对乙物体运动过程由动能定理可得:
-μm乙g(L-x1)=$\frac{1}{2}$m乙v2-$\frac{1}{2}$m乙v乙2,
解得,碰后乙的速度为:v乙=4m/s,
答:(1)物块甲在传送带上滑动产生的热量为400J;
(2)碰撞后一瞬间物块乙的速度为4m/s.
点评 本题考查动量守恒定律及动能定理的应用,过程较为复杂,要注意正确分析物理过程,根据物理过程明确物理规律的选择.

练习册系列答案
相关题目
15.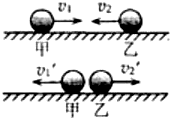 甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
 甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )
甲、乙两物体在光滑水平面上沿同一直线相向运动,甲、乙物体的速度大小分别为3m/s和1m/s;碰撞后甲、乙两物体都反向运动,速度大小均为1.5m/s.则甲、乙两物体质量之比为( )| A. | 2:3 | B. | 2:5 | C. | 3:5 | D. | 5:9 |
20.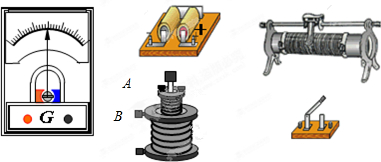 图为(研究电磁感应现象)实验中所用器材的示意图.试回答下列问题:
图为(研究电磁感应现象)实验中所用器材的示意图.试回答下列问题:
(1)按实验要求在右图实物上连线.
(2)在该实验中电流计G的作用是判断是否产生感应电流
(3)填写下列表格.
 图为(研究电磁感应现象)实验中所用器材的示意图.试回答下列问题:
图为(研究电磁感应现象)实验中所用器材的示意图.试回答下列问题:(1)按实验要求在右图实物上连线.
(2)在该实验中电流计G的作用是判断是否产生感应电流
(3)填写下列表格.
| 相关组件的调节状态 | 线圈B中是否有电流 |
| 开关闭合瞬间 | |
| 开关断开瞬间 | |
| 开关闭合后,迅速向左移动滑动变阻器的滑动片 | |
| 开关闭合后,迅速向上拔出线圈A | |
| 开关闭合电路稳定后 |
5. 如图,在边长ab:bc=1:$\sqrt{3}$的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为( )
如图,在边长ab:bc=1:$\sqrt{3}$的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为( )
 如图,在边长ab:bc=1:$\sqrt{3}$的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为( )
如图,在边长ab:bc=1:$\sqrt{3}$的长方形区域abcd内,有垂直纸面向里的匀强磁场,一束速率不同的电子,从b点沿平行边界bc方向射入磁场中,从a点和d点有电子射出磁场,则从a点和d点射出的电子的速率之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{3}$ | D. | 1:4 |
 电视机的显像管中,电子束的偏转是用磁偏转技术实现的.在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过半径为r的圆形区域后,打到荧光屏上,如图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点,已知PO=L,电子的电荷量为e,质量为m.若不计电子所受重力的影响,求:
电视机的显像管中,电子束的偏转是用磁偏转技术实现的.在电子枪中产生的电子经过加速电场加速后射出,从P点进入并通过半径为r的圆形区域后,打到荧光屏上,如图所示.如果圆形区域中不加磁场,电子一直打到荧光屏上的中心O点的动能为E;在圆形区域内加垂直于圆面、磁感应强度为B的匀强磁场后,电子将打到荧光屏的上端N点,已知PO=L,电子的电荷量为e,质量为m.若不计电子所受重力的影响,求: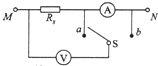 如图所示,用伏安法测电阻Rx时,MN接在恒定电压上,当S接a点时电压表示数为10V,电流表示数为0.2A;当S接b点时,电压表示数为12V,电流表示数为0.15A.求:
如图所示,用伏安法测电阻Rx时,MN接在恒定电压上,当S接a点时电压表示数为10V,电流表示数为0.2A;当S接b点时,电压表示数为12V,电流表示数为0.15A.求: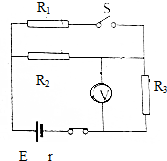 在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.
在如图电路中,电阻R1=R2=R3=1Ω,当S闭合时,电压表示数为1V,当S断开时,电压表示数为0.8V,试求电路中电源的电动势和内阻.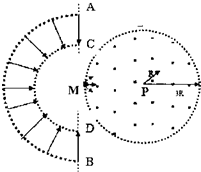 “太空粒子探测器”是由加速、偏转和收集三部分组成.其原理可简化如下:如图所示,辐射状的加速电场区域边界为两个同心平行半圆弧面,圆心为M,外圆弧面AB与内圆弧面CD的电势差为U.图中偏转磁场分布在以P为圆心,半径为3R的圆周内,磁感应强度大小为B,方向垂直纸面向外;内有半径为R的圆盘(圆心在P处)作为收集粒子的装置,粒子碰到圆盘边缘即被吸收.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到AB圆弧面上,并被加速电场从静止开始加速,从M点以某一速率向右侧各个方向射人偏转磁场,不计粒子间的相互作用和其他星球对粒子引力的影响.
“太空粒子探测器”是由加速、偏转和收集三部分组成.其原理可简化如下:如图所示,辐射状的加速电场区域边界为两个同心平行半圆弧面,圆心为M,外圆弧面AB与内圆弧面CD的电势差为U.图中偏转磁场分布在以P为圆心,半径为3R的圆周内,磁感应强度大小为B,方向垂直纸面向外;内有半径为R的圆盘(圆心在P处)作为收集粒子的装置,粒子碰到圆盘边缘即被吸收.假设太空中漂浮着质量为m,电量为q的带正电粒子,它们能均匀地吸附到AB圆弧面上,并被加速电场从静止开始加速,从M点以某一速率向右侧各个方向射人偏转磁场,不计粒子间的相互作用和其他星球对粒子引力的影响.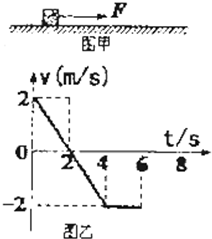 如图甲所示,一质量为1kg的小木块在粗糙的水平地面上作直线运动.物块和地面间动摩擦因数μ=0.2,t=0时刻在水平外力作用下木块向右运动,其速度时间图象如图乙所示,选向右为正方向,运动过程不同时间段里拉力大小和方向可变.求:
如图甲所示,一质量为1kg的小木块在粗糙的水平地面上作直线运动.物块和地面间动摩擦因数μ=0.2,t=0时刻在水平外力作用下木块向右运动,其速度时间图象如图乙所示,选向右为正方向,运动过程不同时间段里拉力大小和方向可变.求: