题目内容
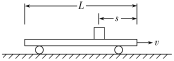
【题目】如图所示,光滑的水平地面上静止放置一长木板,在长木板上的右端和距右端x1=1.6m的P处各放置一个木块A和B(两木块均可视为质点),木块A的质量和长木板的质量均为M=1.8kg,木块B的质量为m=0.6kg,P点右侧长木板的上表面光滑;P点左侧(包括P点)粗糙,木块B与P点左侧长木板间的动摩擦因数为μ=0.2.现有水平向右的恒定拉力F作用在长木板上(图中未画出拉力F),使板由静止开始运动。已知木块B与长木板间的最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2。
![]()
(1)若要求木块B(与木块A相碰前)相对长木板静止,求拉力F应满足的条件;
(2)若F=2.4N,在木块A、B相碰时撤去拉力F,同时锁定长木板使长木板立刻保持静止,且木块A、B间的碰撞是弹性碰撞,最终木块B刚好没有滑离长木板,求P点左侧长木板的长度。
【答案】(1)小于等于4.8N;(2)0.2m
【解析】
(1)设B与木板相对静止的最大加速度为a0,则对系统:F=(M+m)a0
对B:μmg=ma0
联立可得:F=4.8N
即拉力F应满足条件小于等于4.8N
(2)若F=2.4N,则:F=(M+m)a
可得:a=1m/s2
又:v2=2ax1
解得:v=![]() m/s
m/s
A与B碰撞的过程中二者的动量守恒,选取向右为正方向,则:mv=mvB+MvA
由于是弹性碰撞,则:![]()
可得:![]() ,
,![]()
由题意B滑到木板的左端时速度为0,则:![]()
代入数据可得:x2=0.2m

练习册系列答案
相关题目