题目内容
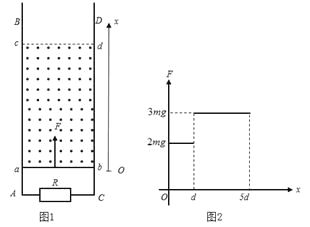
【题目】如图所示,某透明介质的截面由直角三角形AOC和圆心为O、半径为R的四分之一圆BOC组成,其中∠OAC=53°.现让一组平行光由AB边上OD部分垂直射介质。已知该介质的折射率n=![]() ,光在真空中的传播速度为c,sin53°=0.8,cos53°=0.6。
,光在真空中的传播速度为c,sin53°=0.8,cos53°=0.6。
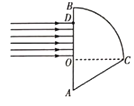
(i)若让这组平行光均能从BC边出射,求这组平行光的最大宽度;
(ii)若OD=0.6R,由D点人射的光线将途经AC边上E点,且AE=0.65R,求该光线在介质中的传播时间。(结果可用根号表示)
【答案】(i)![]() R;(ii)
R;(ii)![]()
【解析】
(i)设临界角为C,则有:sinC=![]() =
=![]()
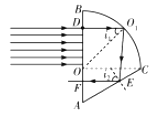
由D点入射的光线至BC边的O1处入射角i1=C时,恰好发生全反射,则这组平行光的最大宽度为:
d=Rsini1=RsinC=![]() R
R
(ii)依题意,由D点入射的光线至BC边的O1处入射角为i1,则有: sini1=0.6,i1=37°
可知,i1>C
光线在O1处发生全反射至AC边上E点处,由几何关系易知OO1∥AC
则有i2=90°-37°=53°>C,再次发生全反射至OA边垂直出射,由等腰三角形可得O1E=R,则光线在介质中的路程为: S=Rcos37°+R+AEcos37°≈2.32R
光线在介质中的传播速度为: v=![]() =
=![]()
故传播时间为: t=![]() =
=![]()

练习册系列答案
相关题目