题目内容
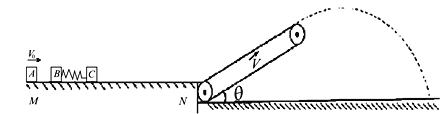
【题目】某种弹射装置的示意图如图所示,光滑的水平导轨MN右端N处与倾斜传送带理想连接,传送带长度L=15.0m,皮带以恒定速率v=5.0m/s顺时针转动.三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,B、C之间有一段轻弹簧刚好处于原长,滑块B与轻弹簧连接,C未连接弹簧,B、C处于静止状态且离N点足够远,现让滑块A以初速度v0=6.0m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短.滑块C脱离弹簧后滑上倾角θ=37o传送带,并从顶端沿传送带方向滑出斜抛落至地面上.已知滑块C与传送带之间的动摩擦因数μ=0.8,重力加速度g=10m/s2, sin37o=0.6, cos37o=0.8.求:
(1)滑块A、B碰撞时损失的机械能;
(2)滑块C在传送带上因摩擦产生的热量Q;
(3)若每次实验开始时滑块A的初速度v0大小不相同,要使滑块C滑离传送带后总能落至地面上的同一位置,则v0的取值范围是什么?(结果可用根号表示)
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:A、B碰撞过程,应用动量守恒定律与能量守恒定律可以机械能损失;设A、B碰撞后,弹簧第一次恢复原长时,根据由动量守恒和机械能守恒求出A、B的速度,在传送带上根据运动学公式求出相对位移进而求出热量;根据物体在传送带上的运动情况结合动量守恒及机械能守恒求出速度范围。
1)设A与B碰撞后共同速度为![]() ,对A、B有:
,对A、B有:
动量守恒![]()
碰撞时损失机械能![]()
解得![]()
(2)设A、B碰撞后,弹簧第一次恢复原长时AB的速度为![]() ,C的速度为
,C的速度为![]()
由动量守恒: ![]()
由机械能守恒: ![]()
解得![]()
C以![]() 滑上传送带,假设匀加速的直线运动位移为x时与传送带共速,由运动学公式
滑上传送带,假设匀加速的直线运动位移为x时与传送带共速,由运动学公式![]()
![]() ,
,
解得![]()
加速运动的时间为t,有![]()
所以相对位移![]()
摩擦生热![]()
(3)设A的最大速度为![]() ,滑块C与弹簧分离时C的速度为
,滑块C与弹簧分离时C的速度为![]() ,AB的速度为
,AB的速度为![]() ,
,
则C在传送带上一直做加速度为![]() 的匀减速直线运动直到P点与传送带共速,有:
的匀减速直线运动直到P点与传送带共速,有: ![]()
![]()
解得![]()
设A的最小速度为![]() ,滑块C与弹簧分离时C的速度为
,滑块C与弹簧分离时C的速度为![]() ,AB的速度为
,AB的速度为![]() ,则C在传送带上一直做加速度为
,则C在传送带上一直做加速度为![]() 的匀加速直线运动直到P点与传送带共速,有:
的匀加速直线运动直到P点与传送带共速,有:
![]()
解得![]() 。
。
对A、B、C和弹簧组成的系统从AB碰撞后到弹簧第一次恢复原长的过程中,有:
动量守恒: ![]()
机械能守恒: ![]()
解得![]() ,同理,
,同理, ![]()
所以![]()