Question

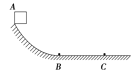
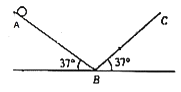
【题目】如图所示，两倾角均为37°的斜面AB、CB平滑对接，斜面长均为4m。一小球从斜面AB的顶端由静止释放，在两斜面上运动，不考虑小球在B点的能量损失。已知小球与斜面AB、BC间的动摩擦因数分别为0.5、0.25，重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8，则下列说法正确的是（　　）

A. 小球第一次到达最低点时的速度为

B. 小球运动后第一次速率为0的位置距B点的距离为2m

C. 小球在斜面AB、BC上运动的总路程之比为

D. 小球在斜面AB、BC上运动时产生的热量之比为

Answer 1

【答案】AC

【解析】

A．小球由A下滑到B的过程中，根据动能定理有：（mgsinθ-μ1mgcosθ）LAB=，解得：vB=4m/s，故A正确；

B．小球沿斜面BC上滑时，根据动能定理有：-（mgsinθ+μ2mgcosθ）L1=0-，解得：L1=1m，故B错误；

CD．小球沿斜面BC下滑又冲上斜面AB的过程中，有：（mgsinθ-μ2mgcosθ）L1-（mgsinθ+μ1mgcosθ）L2=0，解得：L2=0.4m，而且分析可知小球每次由斜面AB下滑到再次滑回斜面AB的过程中，两边路程之比是固定的，即S1：S2=（LAB+L2）：2L1=l1：5，由于在两个斜面上的摩擦力不同，所以在斜面AB、BC上运动时产生的热量之比就不是l1：5，故C正确，D错误。