题目内容
4.如图(1),正三角形金属线框水平放置,总电阻为1Ω,边长为3m,处在两个半径均为1m的圆形匀强磁场区域中.线框顶点与右侧圆中心重合,线框底边中点与左侧圆中心重合.磁感应强度B1垂直水平面向外,大小不变,B2垂直水平面向里,大小随时间变化,B1、B2的值如图(2).则t=0.6s时穿过线框的磁通量为1Wb,t=0.3s时线框整体受到的安培力为13.75N.(取π≈3)
分析 根据磁通量Φ=BS求解,S是有效面积;由于有两种方向的磁感线穿过线框,要根据抵消后的磁通量求.
由法拉第电磁感应定律和欧姆定律求出感应电流的大小,再由F=BIL求解安培力.
解答 解:t=0.6s时,穿过线框的磁通量为:Φ=B2×$\frac{1}{6}$×πr2-B1×$\frac{1}{2}$×πr2=(5×$\frac{1}{6}$×3×12-1×$\frac{1}{2}$×3×12)Wb=1Wb;
t=0时刻穿过线框的磁通量为:Φ0=B1×$\frac{1}{2}$×πr2-B2×$\frac{1}{6}$×πr2=1×$\frac{1}{2}$×3×12-2×$\frac{1}{6}$×3×12Wb=0.5Wb.磁感应强度B1垂直水平面向外,大小不变;B2垂直水平面向里,大小随时间增大,故线框总的磁通量先减小后增大,由楞次定律可得,线框中感应电流方向为逆时针方向,B1磁场中导线所受的安培力方向向左,B2磁场中导线所受的安培力的合力方向向左.
由法拉第电磁感应定律得:线框中产生的感应电动势 E=$\frac{△{B}_{2}}{△t}$×$\frac{1}{6}$×πr2=$\frac{5-2}{0.6}$×$\frac{1}{6}$×3×12=2.5V
感应电流为 I=$\frac{E}{R}$=$\frac{2.5}{1}$A=2.5A
则t=0.3s时线框整体受到的安培力为 F=B1IL+B2Ir=1×2.5×2+3.5×2.5×1=13.75N,方向向左.
故答案为:1,13.75.
点评 本题要紧扣磁通量的定义解答,要注意磁通量的正负,理解法拉第电磁感应定律与闭合电路欧姆定律的应用,及其焦耳定律,注意安培力大小计算与方向的判定.

练习册系列答案
相关题目
15.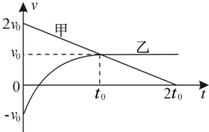 甲、乙两质点同时沿同一直线运动,速度随时间变化的v-t图象如图所示.关于两质点的运动情况,下列说法正确的是( )
甲、乙两质点同时沿同一直线运动,速度随时间变化的v-t图象如图所示.关于两质点的运动情况,下列说法正确的是( )
 甲、乙两质点同时沿同一直线运动,速度随时间变化的v-t图象如图所示.关于两质点的运动情况,下列说法正确的是( )
甲、乙两质点同时沿同一直线运动,速度随时间变化的v-t图象如图所示.关于两质点的运动情况,下列说法正确的是( )| A. | 在t=0时,甲、乙的运动方向相同 | |
| B. | 在0~t0内,乙的加速度先增大后减小 | |
| C. | 在0~2t0内,乙的平均速度等于甲的平均速度 | |
| D. | 若甲、乙从同一位置出发,则t0时刻相距最远 |
12. 如图,离水平地面一定高处水平固定一内壁光滑的圆筒,筒内固定一轻质弹簧,弹簧处于自然长度.现将一小球从地面以某一初速度斜向上抛出,刚好能水平进入圆筒中,不计空气阻力.下列说法中正确的是( )
如图,离水平地面一定高处水平固定一内壁光滑的圆筒,筒内固定一轻质弹簧,弹簧处于自然长度.现将一小球从地面以某一初速度斜向上抛出,刚好能水平进入圆筒中,不计空气阻力.下列说法中正确的是( )
 如图,离水平地面一定高处水平固定一内壁光滑的圆筒,筒内固定一轻质弹簧,弹簧处于自然长度.现将一小球从地面以某一初速度斜向上抛出,刚好能水平进入圆筒中,不计空气阻力.下列说法中正确的是( )
如图,离水平地面一定高处水平固定一内壁光滑的圆筒,筒内固定一轻质弹簧,弹簧处于自然长度.现将一小球从地面以某一初速度斜向上抛出,刚好能水平进入圆筒中,不计空气阻力.下列说法中正确的是( )| A. | 小球在上升过程中处于失重状态 | |
| B. | 弹簧获得的最大弹性势能等于小球抛出时的动能 | |
| C. | 小球从抛出点到筒口的时间与小球抛出时的初速度方向有关 | |
| D. | 小球从抛出点到筒口的时间与小球抛出时的初速度方向无关 |
19.一台电风扇,只有白天有人接近时,电风扇才转动,实现这一功能所需要的传感器为( )
| A. | 声传感器和温度传感器 | B. | 光照传感器和红外线传感器 | ||
| C. | 温度传感器和触发传感器 | D. | 声传感器和触发传感器 |
16.一列简谐横波,在t=0.6s时刻的图象如图甲所示,此时,P、Q两质点的位移均为-1cm,波上A质点的振动图象如图乙所示,则以下说法正确的是( )


| A. | 这列波沿x轴负方向传播 | |
| B. | 这列波的波速是$\frac{50}{3}$m/s | |
| C. | 从t=0.6s开始,紧接着的△t=0.6s时间内,A质点通过的路程是10m | |
| D. | 从t=0.6s开始,质点P比质点Q早0.4s回到平衡位置 |
14.光滑水平面上有一质量为2kg的物体,在五个恒定的水平共点力的作用下处于平衡状态.现同时撤去大小分别为8N和16N的两个水平力而其余力保持不变,关于此后物体的运动情况的说法中正确的是( )
| A. | 一定做匀变速直线运动,加速度大小可能是4m/s2 | |
| B. | 可能做匀减速直线运动,加速度大小可能是2m/s2 | |
| C. | 一定做匀变速运动,加速度大小可能是10m/s2 | |
| D. | 可能做匀速圆周运动,向心加速度大小可能是8m/s2 |
 一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m,则该横波波长为1.2m,波速大小为0.3m/s,波源的起振方向是沿y轴正方向(选填“正”或“负”).
一列简谐横波沿直线传播.以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图所示,已知O、A的平衡位置相距0.9m,则该横波波长为1.2m,波速大小为0.3m/s,波源的起振方向是沿y轴正方向(选填“正”或“负”).
 如图所示,截面为三角形透明介质的三棱镜,三个顶角分别为∠A=60°,∠B=75°,∠C=45°,介质的折射率n=$\sqrt{3}$,现有一束光线沿MN方向射到棱镜的AB面上,入射角的大小i=60°,光在真空中的传播速度c=3×108m/s,求:
如图所示,截面为三角形透明介质的三棱镜,三个顶角分别为∠A=60°,∠B=75°,∠C=45°,介质的折射率n=$\sqrt{3}$,现有一束光线沿MN方向射到棱镜的AB面上,入射角的大小i=60°,光在真空中的传播速度c=3×108m/s,求: