Question

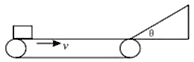
【题目】如图所示，一水平传送带以2.0m/s的速度顺时针转动，水平部分长为1m。其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面足够长，—个可视为质点的物块无初速度地放在传送带最左端。已知物块与传送带间动摩擦因数μ=0.2，sin37°=0.6，g取10m/s2，则（ ）

A.物块在传送带上先做匀加速、后做匀速直线运动

B.物块到达传送带右端的速度大小为1.6m/s

C.物块沿斜面上滑能上升的最大高度为0.2m

D.物块返回皮带时恰好能到达最左端

Answer 1

【答案】CD

【解析】

AB. 可视为质点的物块无初速度地放在传送带最左端，物块在滑动摩擦力作用下在传送带上先做匀加速直线运动，由μmg=mal，加速度a1=2m/s2，速度达到v0=2m/s时运动的位移x1=，即物块到达皮带最右端时恰好与皮带共速，故AB错误；

C.物块以初速度ν0滑上斜面后做匀减速直线运动，根据牛顿第二定律可得，加速度大小a2=gsinθ=6m/s2，当物块速度减为零时上升高度最大，此时沿斜面上滑的距离为s2=；上升的最大高度hm=s2sinθ=0.2m，故C正确；

D.设物块返回皮带时滑动的距离为x，由动能定理

mghm-μmgx=0

解得x=1m，所以物块返回皮带时能到达最左端，故D正确。